题意:定义高度为(x)的金字塔数列为周期为(2x-2)的无限数列。它的每一个周期都是形如(1,2,...,x-1,x,x-1,...,2)的形式。记高度为(x)的金字塔数列第(i)个数为(p_{x,i})
现在给出(n)和(m),求集合(S = {(x,y) | \, exists i , x = A_{n,i}, y = A_{m,i}})的大小。
(n,m leq 10^9)
遇到此题似乎无从下手。在于我们无从直接处理数列。
考虑把((x,y))的二元组放在二维坐标系上。那么,一个金字塔数列就是在来回反弹,而两个就是在二维网格图上来回反弹,直至到达四个终点中的任意一个。这个网格图的边长为(n-1)和(m-1)。于是形成了与坐标轴夹角为(45^{circ})的折线。
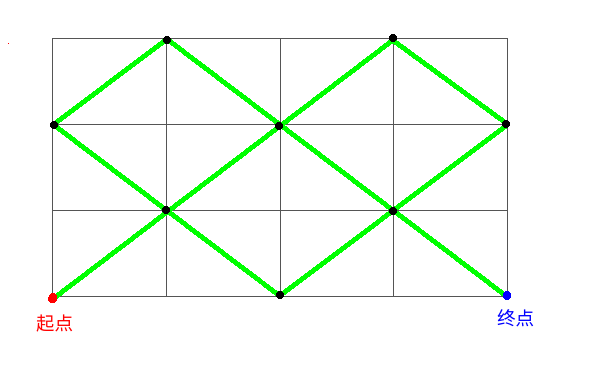
现在,我们要求的就是所到达的格点数量。设图边长分别为(a)和(b)。
问题在于一个结点到达多次只算一次。否则就通过镜面展开的套路,得到答案为(frac {ab} {gcd(a,b)})。这也就是我们所能走的路径长度。
考虑(a,b)互质的情况。那么,我们走的路径长度为(ab)。注意到图上也正好有(ab)个网格。因为我们只沿对角线走,所以所有经过结点的横坐标和纵坐标的和的奇偶性是一定的。考虑一个方格,它边上的4个格点中只有两个是有可能经过的,而要穿过这个方格,就只能走那两个格点的连线。显然,路径上的边是不重的。因此,每个方格最多被经过1次,则路径长度小于等于(ab)。而它事实上正等于(ab),这说明每个网格都被穿过了,那么,所有可能经过的格点都经过了。于是,经过的格点数就是(leftlceil frac {(a+1)(b+1)} {2} ight ceil)。
而当(a,b)不互质时,设(gcd(a,b)=d, \, a = a' d , \, b = b' d),那就相当于把原来的网格放大(d)倍。每个小网格都变成了一个(d imes d) 的大网格。因此,穿过一个大网格时,还会再经过(d-1)个格点,它们只会经过1次。所以答案再加上(a'b' imes (d-1))就可以了。
时间复杂度(O(log n))。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
class PyramidSequences {
public:
long long distinctPairs( int N, int M );
};
long long PyramidSequences::distinctPairs(int N, int M) {
N --;
M --;
ll d = __gcd(N,M);
ll x = N / d, y = M / d;
ll ret = ((x + 1) * (y + 1) + 1) / 2;
ret += x * y * (d-1);
return ret;
}
小结:TC的题目还是很有灵活性的。在数形结合基础上,拓展经典问题,这还是有难度的。