矩阵快速幂基础讲解

1.基础知识储备篇

矩阵的相关运算会再线性代数中学到。
1.1矩阵的定义：
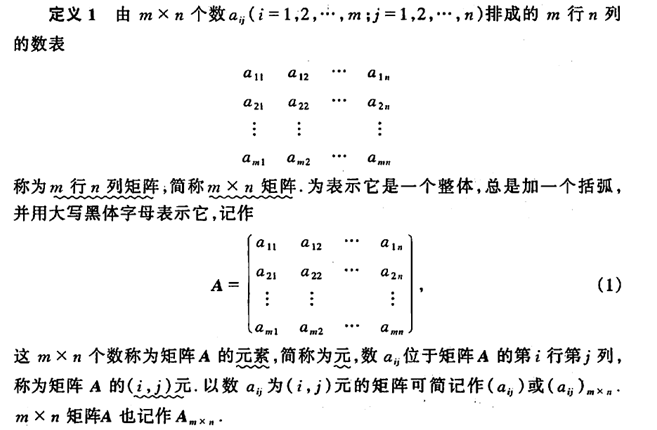 N阶方阵（N阶矩阵）：行数m与列数n相同的矩阵，如下图所示就是一个44的方阵：*

行矩阵（行向量）：只有一行的矩阵，下图就是一个行矩阵：
​

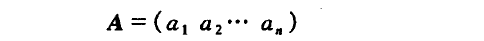
列矩阵（列向量）：只有一列的矩阵，下图就是一个列矩阵：
​

同型矩阵：设先有矩阵A和矩阵B，矩阵A的行数与列数和矩阵B的相同，则矩阵A、B是同型矩阵。

​

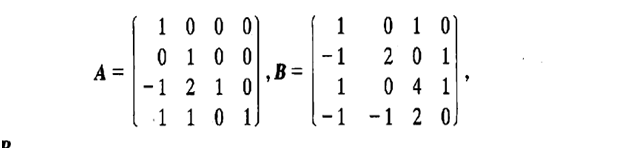
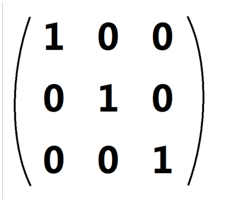
单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1,这种矩阵被称为单位矩阵．它是个方阵，从左上角到右下角的对角线（称为主对角线）上的元素均为1。除此以外全都为0。如下图所示是一个3阶的单位矩阵。
···

1.2矩阵的相关运算：
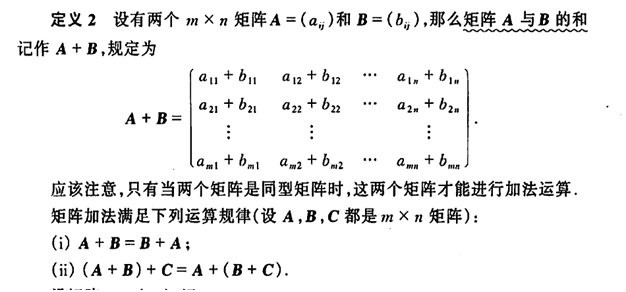
矩阵加法：

矩阵乘法

2.矩阵快速幂引入篇

整数快速幂：
为了引出矩阵的快速幂，以及说明快速幂算法的好处，我们可以先求整数的幂。
如果现在要算X^8：则 XXXXXXXX 按照寻常思路，一个一个往上面乘，则乘法运算进行7次。
(XX)(XX)(XX)(XX)
这种求法，先进行乘法得X^2,然后对X^2再执行三次乘法，这样去计算，则乘法运算执行4次。已经比七次要少。所以为了快速算的整数幂，就会考虑这种结合的思想。
现在要考虑应该怎么分让计算比较快。接下来计算整数快速幂。例如：X^19次方。
19的二进制为：1 0 0 1 1 。
由(X^m)(X^n) = X^(m+n)
则X^19 = (X^16)(X^2)*(X^1)
那么怎么来求解快速幂呢。请看下列代码：
求解X^N的值。
///整数快速幂，计算x^N

int QuickPow(int x,int N)
{
    int res = x;
    int ans = 1;
    while(N)
    {
        if(N&1)
        {
            ans = ans * res;
        }
        res = res*res;
        N = N>>1;
    }
    return ans;
}

那么让我们来看看下面这段代码到底对不对：
对于X^19来说：
19的二进制为：1 0 0 1 1
初始：

ans = 1; res = x;

则10011最后一位是1，所以是奇数。

 ans = res*ans = x; 
res = res*res = x^2;

然后右移一位，1 0 0 1
则1001最后一位是1，所以是奇数

	ans = res*ans = x*(x^2) = x^3     
res = res*res = x^2*x^2 = x^4

然后右移一位，1 0 0
则最后一位是0，所以当前的数为偶数。

	res = res*res = x^4*x^4 = x^8

然后右移一位，1 0
最后一位是0，当前数是偶数。

	res = res*res =x^8*x^8= x^16

然后右移一位，1
最后一位是1，当前数是奇数

	ans = ans*res = (x^3)*（x^16） = x^19
	res = res*res = x^32

可以看出res = X^m,m 始终是与二进制位置上的权值是相对应的。当二进制位为0时，我们只让resres使幂指数2.对应下一个二进制位的权值，当二进制位为1时，ans = ans*res 。则乘上了该乘的X幂次。
2.矩阵快速幂算法篇

看了一个整数数的快速幂，现在我们就正式介绍矩阵快速幂算法。假如现在有一个n*n的方阵A。所谓方阵就是行数和列数相等的矩阵，先给出一个数M，让算矩阵A的M次幂，A^M.在此只要求计算并不需要去深究这个矩阵到底是什么含义。则上面代码可以化为。

上面只是简单的计算矩阵的幂，大家会感觉很抽象，因为上述矩阵并没有具体的含义，
现在就举例说明矩阵快速幂在实际运用中的意义：
以最常见的斐波那契数列为例：众所周知：斐波那契数列递推公式为：
F[n] = F[n-1] + F[n-2]. 由f[0]=0,f[1]=1,可以递推后面的所有数。
在以前，我们会常常用for循环，这是最直接的算法。
POJ 3070 题目，让求斐波那契数列，其n更是高达10亿。
直接递推的局限性：
（1）本题让你递推的斐波那契数n高达10亿。测试时间仅1秒的时间，for循环用递推公式递归导致超时。
（2）想要打表实现随机访问根本不可能，先把斐波那契数列求到10亿，然后想去进行随机访问。题目未给出那么多内存，数组也开不到10亿。
因此它可以用矩阵快速幂来写。
观察f[n] = f[n-1]+f[n-2] 第n相是由第n-1项和第n-2项递推而来。
同理，第n+1项由第n项和第n-1项递推而来。
因此可以用矩阵表示：

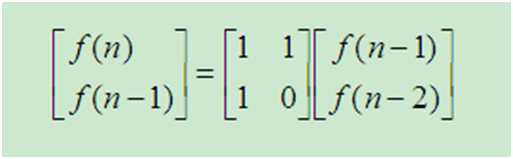
则，知道f[n-1]、f[n-2]则乘上左方矩阵，就能得到等号左侧矩阵，第一个位置
即为要求的f[n]。