问题描述:指派问题
有N台计算机和K个任务。我们可以给每台计算机分配一个任务,每台计算机可以处理的任务种类各不相同。请求出最多能处理的任务的个数。
分析:
这个问题可以转换为图论问题来分析。我们可以定义无向二分图G=(U∪V,E)。
U是代表计算机的顶点集合,V是代表任务的顶点集合,对于任意u∈U和v属于V,计算机u能够处理的任务v<=>(u,v)∈E
而G满足两两不含公共端点的边集合M∈E的基数|M|的最大值,就是我们所要求的最大任务的个数。
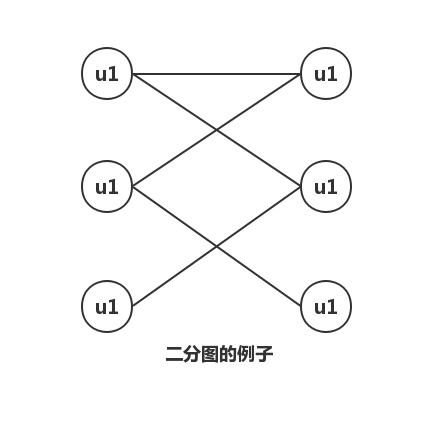
图论术语中,我们将这种两两不含公共端点的边的集合M称为匹配,而元素最多的M则称为最大匹配。当最大匹配的匹配数目满足2|M|=|V|时,又称为完美匹配。特别地,二分图中的匹配又称为二分图匹配。
实际上,可以将二分图最大匹配问题看成是最大流问题的一种特殊情况,不妨对原图作如下变形。
将原图中的所有无向边e改成有向边,方向从U到V,容量为1。增加源点s和汇点t,从s向所有的顶点u∈U连一条容量为1的边,从所有的顶点v∈V向t连一条容量为1的边。
这样变形后的新图G' 中最大s-t流的流量就是原二分图G中最大匹配的匹配数,而U-V之间流量的正的边集合就是最大匹配。

核心代码:
int N,K;
bool can[100][100];
struct edge
{
///分别表示终点,容量,反向边
int to,cap,rev;
};
vector <edge> G[100];///图的邻接表表示
bool used[100];
///向图中增加一条从s到t容量为cap的边
bool add_edge(int from,int to,int cap)
{
G[from].push_back((edge)
{
to,cap,G[to].size()
});
G[to].push_back((edge)
{
from,0,G[from].size()-1
});///反向边的最大的容量应该设置为0,因为这条边本来是不存在的
}
///通过dfs寻找增广路
int dfs(int v,int t,int f)///起点,终点,流量
{
if(v==t) return f;///起点和终点相等的话,流量是没有变化的
used[v]=true;///标记这个点已经走过
for(int i=0; i<G[v].size(); i++)///遍历以这个点为起点的所有的边
{
edge &e=G[v][i];
if(!used[e.to]&&e.cap>0)///这个点没有访问过,并且还有流量呢
{
int d=dfs(e.to,t,min(f,e.cap));///接着往下遍历
if(d>0)///这次遍历所消耗的流量
{
e.cap-=d;
G[e.to][e.rev].cap+=d;
return d;
}
}
}
}
///从s到t的最大流
int max_flow(int s,int t)
{
int flow=0;
for(;;)
{
memset(used,0,sizeof(used));
int f=dfs(s,t,inf);
if(f==0)
return flow;
flow+=f;
}
}
void solve()
{
///0~N-1:计算机对应的顶点
///N~N+K-1:任务对应的顶点
int s=N+K,t=s+1;
///在源点和计算机之间连线
for(int i=0; i<N; i++)
add_edge(s,i,1);
///在任务和汇点之间连线
for(int i=0; i<K; i++)
{
add_edge(i+N,t,1);
}
///在计算机和任务之间连线
for(int i=0; i<N; i++)
for(int j=0; j<K; j++)
{
if(can[i][j])
add_edge(i,j,1);
}
printf("%d
",max_flow(s,t));
}
利用所有边的容量都是1以及二分图的性质,我们还可以将二分图最大匹配算法更简单的实现。
核心代码:
int V; ///顶点数
vector<int> G[100]; ///图的邻接表表示
int match[100]; ///所匹配的顶点
bool used[100]; ///dfs中用到的访问标记
///向图中增加一条连接u和v的边
void add_edge(int u,int v)
{
G[u].push_back(v);
G[v].push_back(u);
}
///通过dfs寻找增广路
bool dfs(int v)
{
used[v]=true;
for(int i=0;i<G[v].size();i++)
{
int u=G[v][i],w=match[u];
if(w<0|| !used[w]&&dfs(w))
{
match[u]=v;
match[v]=u;
return true;
}
}
return false;
}
///求解二分图的最大匹配
int bipartite_matching()
{
int res=0;
memset(match,-1,sizeof(match));
for(int v=0;v<V;v++)
{
if(match[v]<0)
{
memset(used,0,sizeof(used));
if(dfs(v))
{
res++;
}
}
}
return res;
}