ST表(稀疏表)
概述
ST表(Sparse Table,稀疏表)是一种主要用于求解可重复贡献问题的数据结构,它基于倍增思想,通过预处理做到快速在线查询,不支持修改
其中可重复贡献问题是指对于一个元素来说,重复计算多次得到的答案不会改变的问题,例如求区间最值(RMQ),求区间最大公约数 ((gcd))等,然而区间和,区间积等问题则不属于可重复贡献问题
过程
预处理
下面我们以区间最大值问题为例,介绍ST表的具体实现
问题:给定长度为 (n) 的序列和 (q) 次询问,每次询问给出 (l,r) ,你需要给出序列 ([l,r]) 区间的最大值
数据范围:对于 (100\%) 的数据,满足 (nin[1,10^5]),(qin[1,2 imes10^5]),(l,rin[1,n]),序列中的任一元素 (a_iin[1,10^9])
首先我们考虑暴力,对于每次询问都扫描 ([l,r]),时间复杂度 (Theta(nm)) 显然T得飞起
那么该怎么解决呢?
考虑预处理出一部分区间的 (max),在询问时只需要将覆盖区间的 (max) 叠加就可以得到答案
那么应该预处理哪些区间呢?
考虑利用倍增思想,每次预处理出以 (i) 为起点,往后数 (2^j) 个数的区间 (max),也就是 ([i,i+2^j-1]) 的区间 (max),不妨设 (f_{i,j}) 表示以 (i) 为起点,往后数 (2^j) 个数的区间 (max)
怎么合并出更大的区间呢?
可以想到把 (2^j) 拆分为两个 (2^{j-1}) 相加,这里可能有些抽象,我们画图来进行更好的理解
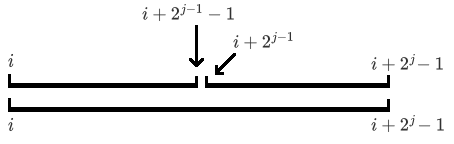
那么有 (f_{i,j}=max(f_{i,j-1},f_{i+2^{j-1},j-1})),类似于DP,只需要递推求解即可
由于需要大量计算对数,每次都使用 (log) 函数十分低效,我们可以把 (log_2) 全部预处理出来,使用的时候直接调用即可,具体方法见代码
c++ code
#define MAXN 100005
int n,f[MAXN][21],lg2[MAXN];//记得定义为全局变量,初始值才是0
for(int i=2;i<=n;++i) lg2[i]=lg2[i>>1]+1;//预处理log_2
for(int i=1;i<=n;++i) scanf("%d",&f[i][0]);//f[i][0]直接读入即可
for(int j=1;j<=lg2[n];++j)//最外层枚举j,相当于每次都翻倍
for(int i=1,tmp=(1<<j)-1;i+tmp<=n;++i)//内层枚举i,遍历这一层数组,从上一层更新
f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]);
查询
对于每一次询问区间 ([l,r]),我们要怎么做才能处理出最大值呢?
我们先计算出满足 (2^kle r-l+1<2^{k+1}) 的 (k),也就是让 (2^k) 小于区间长度的最大的 (k),这样“从 (l) 开始的 (2^k) 个数”以及“以 (r) 结尾的 (2^k) 个数”就一定能覆盖整个询问区间 ([l,r]),也就是“从 (l) 开始的 (2^k) 个数”以及“从 (r-2^k)+1 开始的 (2^k) 个数”
为什么呢?假设这两段无法完全覆盖 ([l,r]) 那么有 (2 imes2^k<|[l,r]|),那么 (k) 就不是让 (2^k) 小于区间长度的最大的 (k),与我们的定义矛盾
“从 (l) 开始的 (2^k) 个数”以及“以 (r) 结尾的 (2^k) 个数”这两段区间中可能会有重叠的部分,计算时会被重复统计,这就是为什么ST表只能用于处理可重复贡献问题
同样,再次上图帮助理解
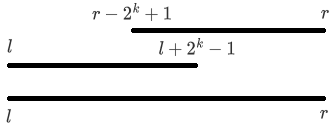
对于每次询问,(f_{l,k}) 和 (f_{r-2^k+1,k}) 的最大值就是 ([l,r]) 的最大值
c++ code
int q,l,r,k;
scanf("%d",&q);
while(q--)//一共q次询问
{
scanf("%d%d",&l,&r);
k=lg2[r-l+1];
printf("%d
",max(f[l][k],f[r-(1<<k)+1][k]));
}
复杂度分析
(注意!以下复杂度分析仅仅适用于RMQ问题,而区间最大公约数的复杂度不在此讨论)
预处理时双层循环,外层枚举 (j),一共枚举 (log_2n) 次,内层枚举 (i),对于每一个 (j) 都要枚举 (n) 次,所以预处理总复杂度为 (Theta(nlog n))
对于每个询问,只用求一次 (max),复杂度为 (Theta(1))
小结
ST表是一种主要用于求解可重复贡献问题的数据结构,尽管能维护的东西有限并且不支持修改操作,但是因为其代码简短,思想清晰,使用方便的特点,在很多地方都有应用,例如求最近公共祖先等等
利用分块思想,笛卡尔树等其他算法或思想还可以对ST表进行优化或拓展,感兴趣的读者可以自行查阅
该文为本人原创,转载请注明出处