Liang-Barsky算法
在Cohen-Sutherland算法提出后,梁友栋和Barsky又针对标准矩形窗口提出了更快的Liang-Barsky直线段裁剪算法。
梁算法的主要思想:
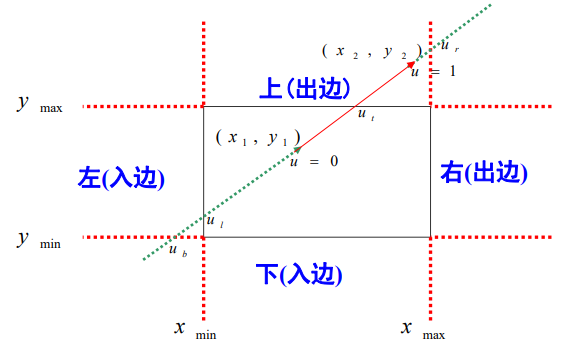
(1)用参数方程表示一条直线
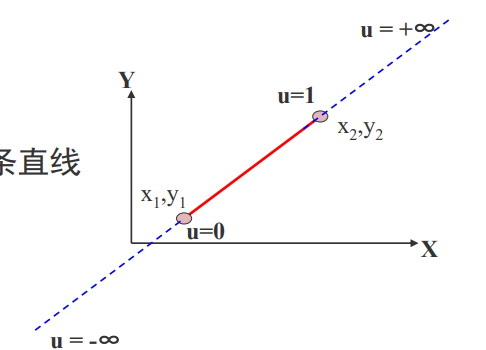

(2)把被裁剪的红色直线段看 成是一条有方向的线段,把窗口 的四条边分成两类:
入边和出边
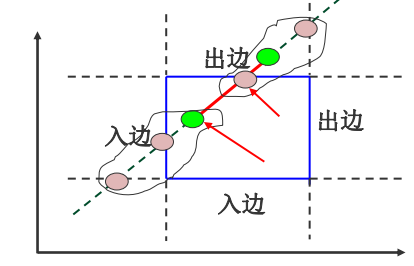
裁剪结果的线段起点是直线和两条入边的交点以及始端点三 个点里最前面的一个点,即参数u最大的那个点;
裁剪线段的终点是和两条出边的交点以及端点最后面的一个 点,取参数u最小的那个点。
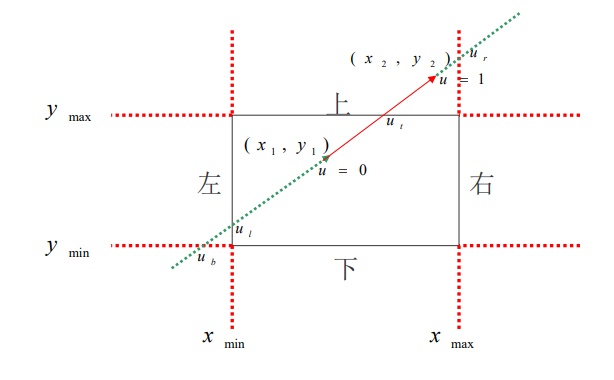
值得注意的是,当u从-∞到+∞遍历直线时,首先对裁剪窗口的两条边界直线(下边和左边)从外面向里面移动,
再对裁 剪窗口两条边界直线(上边和右边)从里面向外面移动。
如果用u1,u2分别表示 线段(u1≤u2)可见部分的开始和结束
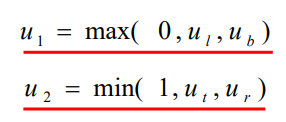
Liang-Barsky算法的基本出发点是直线的参数方程
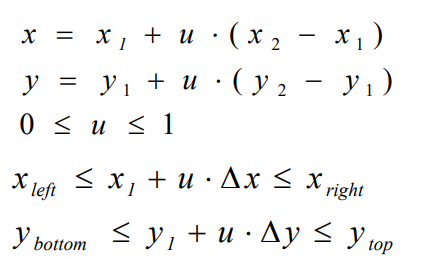
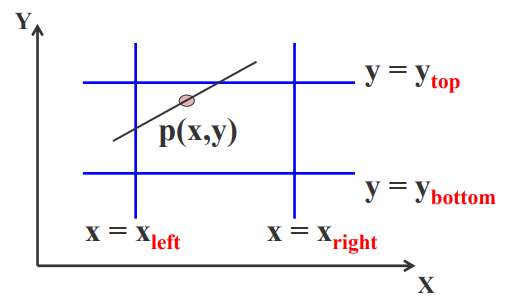



(1)分析Pk=0的情况
如果还满足qk<0
则线段完全在边界外,应舍 弃该线段

如果qk≥0
则进一步判断

(2)当pk≠0时:
当pk<0时
线段从裁剪边界延长线的外部 延伸到内部,是入边交点
当pk > 0时
线段从裁剪边界延长线的内部 延伸到外部,是出边交点
线段和窗口边界一共有四个交点,根据pk的符号,就知道 哪两个是入交点,哪两个是出交点
当p k < 0时:对应入边交点
当p k > 0时:对应出边交点
一共四个u值,再加上u=0、u=1两个端点值,总共六个值
把pk<0的两个u值和0比较去找最大的,把pk>0的两个u值 和1比较去找最小的,这样就得到两个端点的参数值

