codeforces

DZY Loves Physics

DZY loves Physics, and he enjoys calculating density.

Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:

where v is the sum of the values of the nodes, e is the sum of the values of the edges.

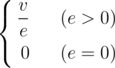
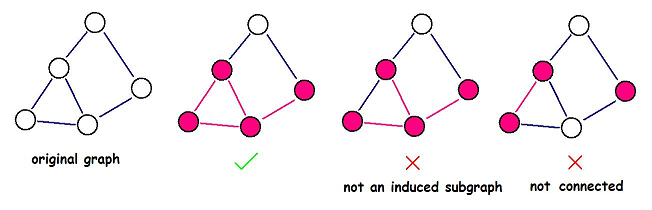
Once DZY got a graph G, now he wants to find a connected induced subgraph G' of the graph, such that the density of G' is as large as possible.

An induced subgraph G'(V', E') of a graph G(V, E) is a graph that satisfies:

• ;
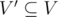• edge 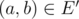 if and only if 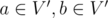, and edge ;
• the value of an edge in G' is the same as the value of the corresponding edge in G, so as the value of a node.

Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.

Input

The first line contains two space-separated integers n (1 ≤ n ≤ 500), 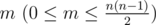. Integer n represents the number of nodes of the graph G, m represents the number of edges.

The second line contains n space-separated integers xi (1 ≤ xi ≤ 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.

Each of the next m lines contains three space-separated integers ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103), denoting an edge between node ai and bi with value ci. The graph won't contain multiple edges.

Output

Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.

Sample test(s)

input

1 0
1

output

0.000000000000000

input

2 1
1 2
1 2 1

output

3.000000000000000

input

5 6
13 56 73 98 17
1 2 56
1 3 29
1 4 42
2 3 95
2 4 88
3 4 63

output

2.965517241379311

Note

In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.

In the second sample, choosing the whole graph is optimal.

最大的肯定是只有一条边的子图，然后枚举。

#include <map>
#include <set>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <queue>
#include <iostream>
#include <stack>
#include <cmath>
#include <string>
#include <vector>
#include <cstdlib>
//#include <bits/stdc++.h>
//#define LOACL
#define space " "
using namespace std;
//typedef long long LL;
typedef __int64 Int;
typedef pair<int, int> paii;
const int INF = 0x3f3f3f3f;
const double ESP = 1e-5;
const double PI = acos(-1.0);
const int MOD = 1e9 + 7;
const int MAXN = 1e5 + 10;
double v[MAXN], e;
int main() {
    int n, m, a, b;
    while (scanf("%d%d", &n, &m) != EOF) {
        for (int i = 1; i <= n; i++) {
            scanf("%lf", &v[i]);
        }
        double maxx = 0;
        for (int i = 0; i < m; i++) {
            scanf("%d%d%lf", &a, &b, &e);
            maxx = max(maxx, (v[a]+v[b])/e);
        }
        printf("%.10lf
", maxx);
    }
    return 0;
}