zoukankan html css js c++ java

[LeetCode] 221. Maximal Square

Given an m x n binary matrix filled with 0's and 1's, find the largest square containing only 1's and return its area.

Example 1:

Input: matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
Output: 4

Example 2:

Input: matrix = [["0","1"],["1","0"]]
Output: 1

Example 3:

Input: matrix = [["0"]]
Output: 0

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 300
matrix[i][j] is '0' or '1'.

最大正方形。

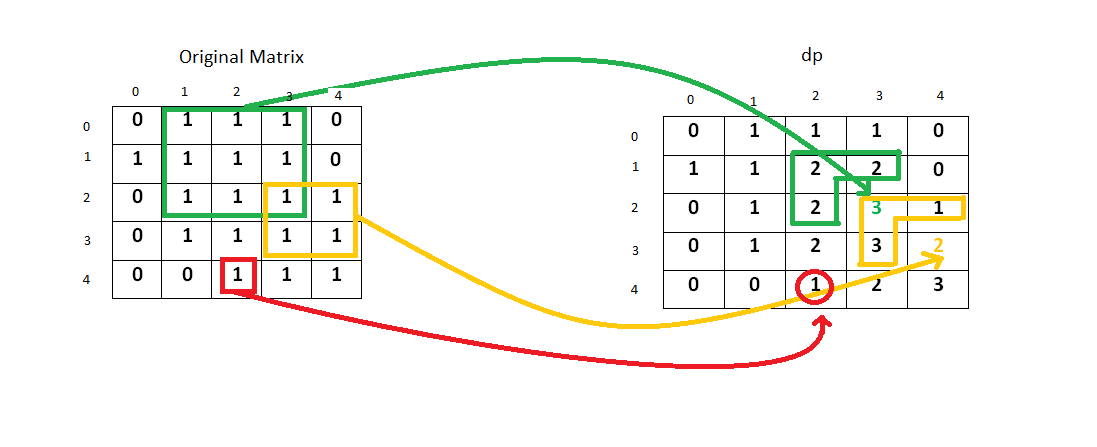
在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。这是一道矩阵类的DP问题。dp[i][j]的定义是以坐标[i][j]为右下角的点组成的正方形的最大边长。状态转移方程是dp(i, j) = min(dp(i−1, j), dp(i−1, j−1), dp(i, j−1)) + 1。这样的题目练多了才会有思路。下图帮助理解DP矩阵是怎么被完成的。

时间O(n^2)

空间O(n^2)

Java一维实现

 1 class Solution {
 2     public int maximalSquare(char[][] matrix) {
 3         int m = matrix.length;
 4         int n = m > 0 ? matrix[0].length : 0;
 5         int[] dp = new int[n + 1];
 6         int max = 0;
 7         int prev = 0;
 8         for (int i = 1; i <= m; i++) {
 9             for (int j = 1; j <= n; j++) {
10                 int temp = dp[j];
11                 if (matrix[i - 1][j - 1] == '1') {
12                     dp[j] = Math.min(Math.min(dp[j - 1], prev), dp[j]) + 1;
13                     max = Math.max(max, dp[j]);
14                 } else {
15                     dp[j] = 0;
16                 }
17                 prev = temp;
18             }
19         }
20         return max * max;
21     }
22 }

Java二维实现

 1 class Solution {
 2     public int maximalSquare(char[][] matrix) {
 3         if (matrix.length == 0) return 0;
 4         int m = matrix.length;
 5         int n = matrix[0].length;
 6         int res = 0;
 7         int[][] dp = new int[m + 1][n + 1];
 8         for (int i = 1; i <= m; i++) {
 9             for (int j = 1; j <= n; j++) {
10                 if (matrix[i - 1][j - 1] == '1') {
11                     dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
12                     res = Math.max(res, dp[i][j]);
13                 }
14             }
15         }
16         return res * res;
17     }
18 }