HNOI2019fish

({ m fish})

20分：

六个for，点积判锐角钝角。

#include <vector>
#include <queue>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define LL long long
#define uint unsigned int
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define GO debug("GO
")
#define rep(i, a, b) for (register uint (i) = (a); (i) <= (b); ++ (i))
#define dep(i, a, b) for (register uint (i) = (a); (i) >= (b); -- (i))

namespace io {
    const char endl = '
';
    template<typename T> inline void chkmin(T &a, T b) { a > b ? a = b : 0; }
    template<typename T> inline void chkmax(T &a, T b) { a < b ? a = b : 0; }
    struct Stream {
        template<class T> Stream operator>> (T &x) { 
            register int f = 1; register char c;
            while (!isdigit(c = getchar())) if (c == '-') f = -1;
            while (x = (x << 1) + (x << 3) + (c ^ 48), isdigit(c = getchar()));
            return x *= f, *this;
        }
        Stream operator>> (char *str) { return scanf("%s", str), *this; }
        template<class T> Stream operator<< (T x) {
            static char out[35]; static uint top = 0; 
            if (x < 0) x = -x, out[++top] = '-';
            while (out[++top] = x % 10 ^ 48, x /= 10, x); 
            while (putchar(out[top--]), top);
            return *this;
        }
        Stream operator<< (char *str) { return printf("%s", str), *this; }
        Stream operator<< (char ch) { return putchar(ch), *this; }
    } cin, cout;
}

const int N = 20;

struct Vector {
    int x, y;
    Vector() {}
    Vector(int _x, int _y) { x = _x, y = _y; }
    Vector operator-(Vector B) { return Vector(x - B.x, y - B.y); }
    Vector operator+(Vector B) { return Vector(x + B.x, y - B.y); }
    int operator*(Vector B) { return x * B.x + y * B.y; }
    int len2() { return x * x + y * y; }
} P[N];

int main() {
#ifndef ONLINE_JUDGE
    freopen("xhc.in", "r", stdin);
    freopen("xhc.out", "w", stdout);
#endif
    register int n, ans = 0;
    std::cin >> n;
    rep(i, 1, n) std::cin >> P[i].x >> P[i].y;
    rep(A, 1, n) rep(B, 1, n) rep(C, 1, n) rep(D, 1, n) rep(E, 1, n) rep(F, 1, n) {
        if (A == B || A == C || A == D || A == E || A == F) continue;
        if (B == C || B == D || B == E || D == F) continue;
        if (C == D || C == E || C == F) continue;
        if (D == E || D == F) continue;
        if (E == F) continue;
        if ((P[B] - P[A]) * (P[D] - P[A]) > 0 and 
                (P[D] - P[A]) * (P[C] - P[A]) > 0 and
                (P[B] - P[D]) * (P[A] - P[D]) > 0 and 
                (P[C] - P[D]) * (P[A] - P[D]) > 0 and 
                (P[A] - P[D]) * (P[E] - P[D]) < 0 and
                (P[A] - P[D]) * (P[F] - P[D]) < 0 and
                (P[A] - P[B]).len2() == (P[A] - P[C]).len2() and
                (P[B] - P[D]).len2 ()== (P[D] - P[C]).len2() and
                (P[E] - P[D]).len2() == (P[D] - P[F]).len2()) {
            ans ++;
        }
    }
    io::cout << ans << io::endl;
    return 0;
}

40分：

对着题面中的图讲，

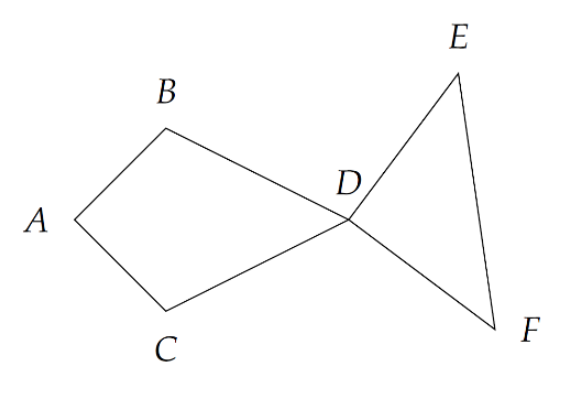
第一部分：

枚举 (A, D) 然后再枚举 P (形如E,F的点)将所有 PD 满足 角ADP 为钝角的 PD 的长扔进一个 vector，

然后 sort，用 f[A][D] 表示 AD 为脊柱，的尾巴数量，由于 sort 了，很好计算出来。

再用 map 实现一个 AD斜率->vector 的映射，vector存斜率为这个的(A, D)。

第二部分：

枚举 (B, C) ，求出 AD斜率 (垂直) ，到 对应的斜率的vector (map映射)中寻找符合题意的 (A, D) ，然后 Ans 加上 f[A][D].

根据题意，最后 Ans *= 4.

#include <vector>
#include <map>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define LL long long
#define uint unsigned int
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define GO debug("GO
")
#define rep(i, a, b) for (register uint i = a, i##end = b; i <= i##end; ++ i)
#define dep(i, a, b) for (register uint i = a, i##end = b; i >= i##end; -- i)

namespace io {
    const char endl = '
';
    template<typename T> inline void chkmin(T &a, T b) { a > b ? a = b : 0; }
    template<typename T> inline void chkmax(T &a, T b) { a < b ? a = b : 0; }
    struct Stream {
        template<class T> Stream operator>> (T &x) { 
            x = 0; register int f = 1; register char c;
            while (!isdigit(c = getchar())) if (c == '-') f = -1;
            while (x = (x << 1) + (x << 3) + (c ^ 48), isdigit(c = getchar()));
            return x *= f, *this;
        }
        Stream operator>> (char *str) { return scanf("%s", str), *this; }
        template<class T> Stream operator<< (T x) {
            static char out[35]; static uint top = 0; 
            if (x < 0) x = -x, out[++top] = '-';
            while (out[++top] = x % 10 ^ 48, x /= 10, x); 
            while (putchar(out[top--]), top);
            return *this;
        }
        Stream operator<< (char *str) { return printf("%s", str), *this; }
        Stream operator<< (char ch) { return putchar(ch), *this; }
    } cin, cout;
}

const int N = 400 + 10;

struct vector {
    int x, y;
    vector(int x = 0, int y = 0) : x(x), y(y) {}
    vector operator-(const vector B) { return vector(x - B.x, y - B.y); }
    LL operator*(const vector B) { return 1ll * x * B.x + 1ll * y * B.y; }
    LL len2() { return 1ll * x * x + 1ll * y * y; }
} p[N];

const uint INF = 0x3f3f3f3f;
int n;
LL f[N][N];
std::vector<int> buc;
std::map<std::pair<int, int>, std::vector<std::pair<int, int> > > Map;

int main() {
#ifndef ONLINE_JUDGE
    freopen("fish.in", "r", stdin);
    freopen("fish.out", "w", stdout);
#endif
    io::cin >> n;
    rep(i, 1, n) io::cin >> p[i].x >> p[i].y;
    rep(A, 1, n) {
        rep(D, 1, n) if (A != D) {
            buc.clear();
            rep(P, 1, n) if (P != A and P != D) {
                if ((p[P] - p[D]) * (p[A] - p[D]) < 0) {
                    buc.push_back((p[P] - p[D]).len2());
                }
            }
            std::sort(buc.begin(), buc.end());
            uint i = 0;
            while (i < buc.size()) {
                uint j = i;
                while(i < buc.size() - 1 and buc[i] == buc[i + 1]) {
                    i++;
                }
                f[A][D] += 1ll * (i - j + 1) * (i - j) / 2;
                i++;
            }
            int up = p[D].y - p[A].y, down = p[D].x - p[A].x, gcd;
            gcd = std::__gcd(abs(up), abs(down));
            if (gcd) 
                Map[std::make_pair(up / gcd, down / gcd)].push_back(std::make_pair(A, D));
            else if (up == 0)
                Map[std::make_pair(0, INF)].push_back(std::make_pair(A, D));
            else 
                Map[std::make_pair(INF, 0)].push_back(std::make_pair(A, D));
        }
    }
    LL Ans = 0;
    rep(B, 1, n) {
        rep(C, 1, n) {
            int up = p[B].y - p[C].y, down = p[B].x - p[C].x, gcd;
            gcd = std::__gcd(abs(up), abs(down));
            std::pair<int, int> Kad;
            if (gcd) 
                Kad = std::make_pair(-down / gcd, up / gcd);
            else if (up == 0) 
                Kad = std::make_pair(INF, 0);
            else 
                Kad = std::make_pair(0, INF);
            for (auto i : Map[Kad]) {
                register uint A = i.first, D = i.second;
                if ((p[B] - p[A]).len2() == (p[C] - p[A]).len2() and 
                        (p[B] - p[D]).len2() == (p[C] - p[D]).len2() and
                        (p[B] - p[A]) * (p[D] - p[A]) > 0 and
                        (p[C] - p[A]) * (p[D] - p[A]) > 0 and
                        (p[B] - p[D]) * (p[A] - p[D]) > 0 and 
                        (p[C] - p[D]) * (p[A] - p[D]) > 0) {
                    Ans += f[A][D];
//                    io::cout << A << ' ' << B << ' ' << C << ' ' << D << io::endl;
//                    io::cout << f[A][D] << io::endl;
                }
            }
        }
    }
    std::cout << Ans * 4 << io::endl;
}

100分

40分复杂度的瓶颈在于计算以AD为脊柱的尾巴的个数，由于我们发现合法的尾巴只可能在垂直AD的直线的右侧，所以考虑先枚举D，按极角排序，再枚举A，让A围着D逆时针转，同时维护合法平面内的尾巴数量，维护的方式与莫队的方法类似。

然后同样枚举AD，为了为了快速求出合法的BC的数量，需要事先处理出任意两点中垂线的解析式，那么鱼的脊柱肯定在BC的中垂线上，所以枚举AD时，通过对AD这条直线所包含的点二分查找就可以知道有多少对BC，再乘以尾巴的数量即可，这里的实现比较复杂，用map映射直线所代表的vector，vector存BC的中点，具体难以描述, 细节就是特判没有斜率的情况。

#include <vector>
#include <map>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>

#define LL long long
#define uint unsigned int
#define debug(...) fprintf(stderr, __VA_ARGS__)
#define GO debug("GO
")
#define rep(i, a, b) for (register uint i = a, i##end = b; i <= i##end; ++ i)
#define dep(i, a, b) for (register uint i = a, i##end = b; i >= i##end; -- i)
#define int LL

namespace io {
    const char endl = '
';
    template<typename T> inline void chkmin(T &a, T b) { a > b ? a = b : 0; }
    template<typename T> inline void chkmax(T &a, T b) { a < b ? a = b : 0; }
    struct Stream {
        template<class T> Stream operator>> (T &x) { 
            x = 0; register int f = 1; register char c;
            while (!isdigit(c = getchar())) if (c == '-') f = -1;
            while (x = (x << 1) + (x << 3) + (c ^ 48), isdigit(c = getchar()));
            return x *= f, *this;
        }
        Stream operator>> (char *str) { return scanf("%s", str), *this; }
        template<class T> Stream operator<< (T x) {
            static char out[35]; static uint top = 0; 
            if (x < 0) x = -x, out[++top] = '-';
            while (out[++top] = x % 10 ^ 48, x /= 10, x); 
            while (putchar(out[top--]), top);
            return *this;
        }
        Stream operator<< (char *str) { return printf("%s", str), *this; }
        Stream operator<< (char ch) { return putchar(ch), *this; }
    } cin, cout;
}

const long double PI = acos(-1), eps = 1e-10;
const int N = 1e3 + 10;

struct vector {
    int x, y, id;
    long double atan;
    vector(int x = 0, int y = 0) : x(x), y(y) {}
    vector operator-(const vector B) { return vector(x - B.x, y - B.y); }
    LL operator*(const vector B) { return 1ll * x * B.x + 1ll * y * B.y; }
    LL len2() { return 1ll * x * x + 1ll * y * y; }
} p[N], vec[N * 2];

struct frac {
    LL u, d;
    void simp() { LL gcd = std::__gcd(u, d); if (gcd) u /= gcd, d /= gcd; if (d < 0) d = -d, u = -u; }
    bool operator< (const frac& B) const { return u < B.u || (u == B.u and d < B.d); }
    bool operator== (const frac& B) const { return (u == B.u and d == B.d); }
};

struct line {
    frac k, b;
    bool operator<(const line& B) const { if(k == B.k) return b < B.b; else return k < B.k; }
} ;

bool cmp(const vector &a, const vector &b) { 
    return a.atan < b.atan;
}

const uint INF = 0x3f3f3f3f;

int n, cnt, sum;
LL f[N][N];
std::map<line, int> Map;
std::map<LL, int> Cnt;
std::vector<int> buc[N * N];

void add(int x) {
    sum += Cnt[vec[x].len2()]++;
}
void del(int x) {
    sum -= --Cnt[vec[x].len2()];
}

signed main() {
#ifndef ONLINE_JUDGE
    freopen("fish100.in", "r", stdin);
    freopen("fish100.out", "w", stdout);
#endif
    io::cin >> n;
    rep(i, 1, n) io::cin >> p[i].x >> p[i].y;
    rep(i, 1, n) {
        rep(j, i + 1, n) {
            if (p[i].y == p[j].y) {
                if ((p[i].x + p[j].x) & 1) continue;
                line L;
                L.k = (frac) { INF, 0 }, L.b = (frac) { (p[i].x + p[j].x) / 2, 1 };
                if (Map.find(L) == Map.end()) Map[L] = ++cnt;
                buc[Map[L]].push_back(p[i].y * 2);
            } else {
                line L;
                L.k = (frac) { p[i].x - p[j].x, p[j].y - p[i].y }; L.k.simp();
                L.b = (frac) { 1ll * (p[i].y + p[j].y) * (p[i].y - p[j].y) + 1ll * (p[i].x + p[j].x) * (p[i].x - p[j].x), 2ll * (p[i].y - p[j].y) }; L.b.simp();
                if (Map.find(L) == Map.end()) Map[L] = ++cnt;
                buc[Map[L]].push_back(p[i].x == p[j].x ? p[i].x * 2 : p[i].y + p[j].y);
            }
        }
    }
    rep(i, 1, cnt) sort(buc[i].begin(), buc[i].end());
    rep(i, 1, n) {
        int tot = 0;
        rep(j, 1, n) {
            if (i != j) {
                vec[++tot] = p[j] - p[i];
                vec[tot].atan = atan2(vec[tot].y, vec[tot].x);
                vec[tot].id = j;
            }
        }
        std::sort(vec + 1, vec + 1 + tot, cmp);
        rep(i, 1, tot) vec[i + tot] = vec[i], vec[i + tot].atan += PI * 2;
        Cnt.clear();
        sum = 0;
        for (int j = 1, begin = 0, end = 0; j <= tot; ++ j) { // (, ]
            while (begin <= tot * 2 and vec[begin + 1].atan < vec[j].atan + 0.5 * PI + eps) begin++, del(begin);
            while (end <= tot * 2 and vec[end + 1].atan + eps < vec[j].atan + 1.5 * PI) end++, add(end);
            f[vec[j].id][i] = sum;
        }
    }
    LL ans = 0;
    rep(i, 1, n) {
        rep(j, i + 1, n) {
            int a, b;
            if (p[i].y == p[j].y) a = std::min(p[i].x, p[j].x), b = std::max(p[j].x, p[i].x);
            else a = std::min(p[i].y, p[j].y), b = std::max(p[i].y, p[j].y);
            line L;
            if (p[i].x == p[j].x) {
                L.k = (frac) { INF, 0 };
                L.b = (frac) { p[i].x, 1 };
            } else {
                L.k = (frac) { p[i].y - p[j].y, p[i].x - p[j].x }; L.k.simp();
                L.b = (frac) { 1ll * p[i].y * (p[i].x - p[j].x) + p[i].x * (p[j].y - p[i].y), p[i].x - p[j].x }; L.b.simp();
            }
            if (Map.find(L) == Map.end()) continue;
            int c = Map[L];
            ans += 1ll * (std::upper_bound(buc[c].begin(), buc[c].end(), b * 2 - 1) - 
                    std::upper_bound(buc[c].begin(), buc[c].end(), a * 2)) * (f[i][j] + f[j][i]);
        }
    }
    io::cout << ans * 4 << io::endl;
    return 0;
}