Description
Solution
如果单独考虑一行i,则左边位置的数严格比右边位置的数小。而一行有m个位置,它们可以填[0,m]这m+1个数,则必然有一个数不存在。
定义第i行的第j位突变需要满足$x[i][j+1]-x[i][j]>1$,此时不存在的数为j。
通过分析可以得到,假如在i-1行的突变位置为j+1,则第i行突变位置的合法范围为[j,m]。*
设f[i][j]为在第i行,突变位置为j的情况数。
则递推式为:$f[i][j]=f[i-1][j+1]+f[i][j-1]$。
因为当第i-1行在第j+1位突变,第i行的突变位置即为j。f[i][j-1]为在[0,j-1]位突变的情况数,由*可得知这些情况也同样可以在第j位突变。
特殊的,$f[i][0]=f[i-1][0]+f[i-1][1]$,$f[i][m]=f[i][m-1]$。
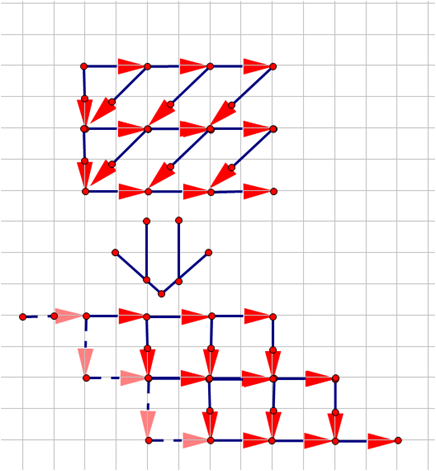
如图,我们把转移画出来后将第i行往右移i-1格并建立虚拟节点来满足f[i][0]的转移。
图中的n=3,m=3。
此时的点(n,n+m+1)[即为第n行第n+m个点]表示的并不是所有情况之和,而是第n行突变位置为m的情况数。
我们考虑多加一行一列,根据递推式,点(n+1,n+m+2)即为第n行所有情况之和了。
最后将得到图形补全为矩形后是会有n+1行n+m+2列。
将该图画在平面直角坐标系里(即将其翻转),则终点坐标为(n,n+m+1)

如图,直线ya=x+1和直线yb=x-(m+2)即为边界。
我们把多次越过同一边界视为只越过一次。则越界方案为ababa...或babab...。
则ans=总方案数-第一次越过a的次数-第一次越过b的次数。
对于先越过a的,考虑:-越界方案末尾为a的情况数+越界方案末尾为ba的方案数-越界方案末尾为aba的方案数。。。直到方案数为0。
对于越界方案末尾为a的情况数,为将整个图针对直线a翻转后(1,1)到对称终点的方案;当越界方案末尾为ba,则在上一个图的基础上把图沿着直线b翻转,计算(1,1)到本次到对称终点的方案数。
Code
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; typedef long long ll; const int mod=1e9+7; int n,m; ll fac[12000010],inv[12000010]; void pre() { fac[0]=inv[0]=1; fac[1]=inv[1]=1; for (int i=2;i<=12000000;i++) { fac[i]=fac[i-1]*i%mod; inv[i]=(mod-mod/i)*inv[mod%i]%mod; } for (int i=1;i<=12000000;i++) inv[i]=inv[i]*inv[i-1]%mod; } ll C(int x,int y) { if (x<y||x<0||y<0) return 0; return fac[x]*inv[y]%mod*inv[x-y]%mod; } ll cal(int x,int y) { if (x<0||y<0) return 0;return C(x+y,y); } void turnA(int &x,int &y) { swap(x,y); x--;y++; } void turnB(int &x,int &y) { swap(x,y);x+=m+2;y-=m+2; } ll ans; int main() { scanf("%d%d",&n,&m); pre(); ans=cal(n+m+1,n); int x=n+m+1,y=n; while (x>=0&&y>=0) { turnA(x,y);ans=(ans-cal(x,y))%mod; turnB(x,y);ans=(ans+cal(x,y))%mod; } x=n+m+1,y=n; while (x>=0&&y>=0) { turnB(x,y);ans=(ans-cal(x,y))%mod; turnA(x,y);ans=(ans+cal(x,y))%mod; } if (ans<0) ans+=mod; cout<<ans; }