<1>矩阵是3D数学的重要基础。它主要用来描述两个坐标系统间的关系,通过定义一种运算而将一个坐标系中的向量转化到另一个坐标系。龟龟
<2>向量是标量的数组,矩阵则是向量的数组
<3>矩阵维度:
一个4X3矩阵例子:
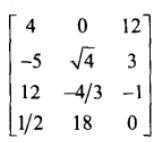
方阵:行数和列数相同的矩阵称作方阵
<4>单位矩阵:
对角矩阵:在说单位矩阵之前,先看什么是对角矩阵:如果所有非对角线元素都为0,那么称这种矩阵为对角矩阵,例如:

单位矩阵:是一种特殊的对角矩阵,n维单位矩阵记作In,是nXn矩阵,对角线元素为1,其他元素为0.例如:3X3单位矩阵
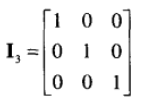 单位矩阵非常特殊,在矩阵乘法中:任意一个矩阵乘以单位矩阵,都将得到原矩阵,从某种意义上,单位矩阵犹如1对于标量的作用
单位矩阵非常特殊,在矩阵乘法中:任意一个矩阵乘以单位矩阵,都将得到原矩阵,从某种意义上,单位矩阵犹如1对于标量的作用
<5>向量用矩阵表示:
因为矩阵可以是mXn,m行n列;那么向量可以用矩阵表示为:向量v(x,y,z) 矩阵表示: [x,y,z] 1行3列矩阵 或者 竖着[x,y,z] 3行1列(这里没有竖着写)
<6>矩阵转置:
矩阵转置:现有一个矩阵rXc矩阵M。M的转置记作Mt,Mt是一个c*r矩阵,它的行是M的列,它的列是M的行。从另一个方面理解,就是沿着M矩阵的对角线翻折了,例如:
 对于任意矩阵M:(Mt)t = M,矩阵转置之后再转置一次就得到原矩阵;对于任意对角矩阵D,都有Dt=D,因为它对角线之外的其他元素都是0
对于任意矩阵M:(Mt)t = M,矩阵转置之后再转置一次就得到原矩阵;对于任意对角矩阵D,都有Dt=D,因为它对角线之外的其他元素都是0
向量矩阵转置:上面说了,一个向量可以用矩阵表示:对于向量来说,转置使行向量变成列向量,使列向量变成行向量;例如:
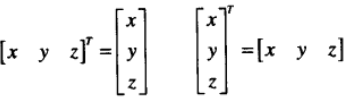
<7>矩阵乘法:
与标量:矩阵M与标量k相乘: 就是矩阵每个元素*k啦

与矩阵:矩阵A乘以矩阵B: 必须满足条件,A是r*n矩阵 B是n*c矩阵 前面的列与后面的行必须相同,得到的结果记作AB(rXc);但是这个时候B乘以A是不可以的,因为n*c r*n c和r不想等
下面看一个矩阵相乘,A为4X2矩阵,B为2X5矩阵,那么AB为4X5矩阵:
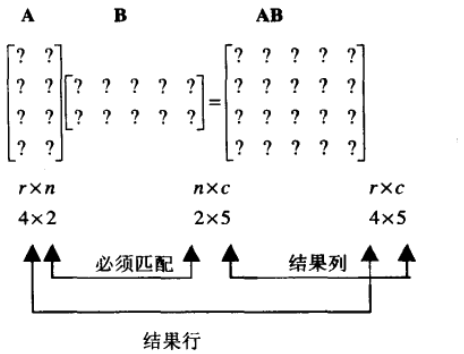
下面引出矩阵相乘运算规则:矩阵A rXn 与 矩阵B nXc的积记作AB rXc为C。C的任意元素Cij等于A的第i行向量与B的第j行向量点乘的结果。记作:

下面展示一个C24的计算:

<8>矩阵相乘2:
2X2矩阵完整公式:
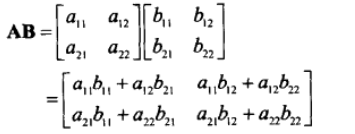
3X3矩阵完整公式:
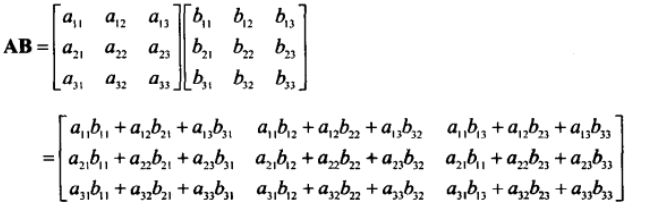
注意:假设下面所说矩阵相乘有意义,任意矩阵M乘以方阵S,不管从哪边乘,都将得到与原矩阵大小相同的矩阵。如果S是单位矩阵,结果仍然就原矩阵,即:M*S= S*M = M(单位矩阵就像1对于标量一样)
矩阵A,B :(AB)t = BtAt
矩阵和向量相乘:M矩阵 v向量也要满足 rXn n*c 不然就没有意义无法相乘了
比如3X3的M矩阵和[x,y,z]行向量1X3 M*V无法相乘 但是V*M是可以的;
意义:矩阵中的每个元素决定了输入向量中的特定元素再输出向量中占的比重。如,m11决定了输入x对输出x值的贡献。