An April Fool's week
- Jordan Smiley(April Fools Day Contest 2020 E)
给你一张图片,判断((x,y))是否在脸里面。。
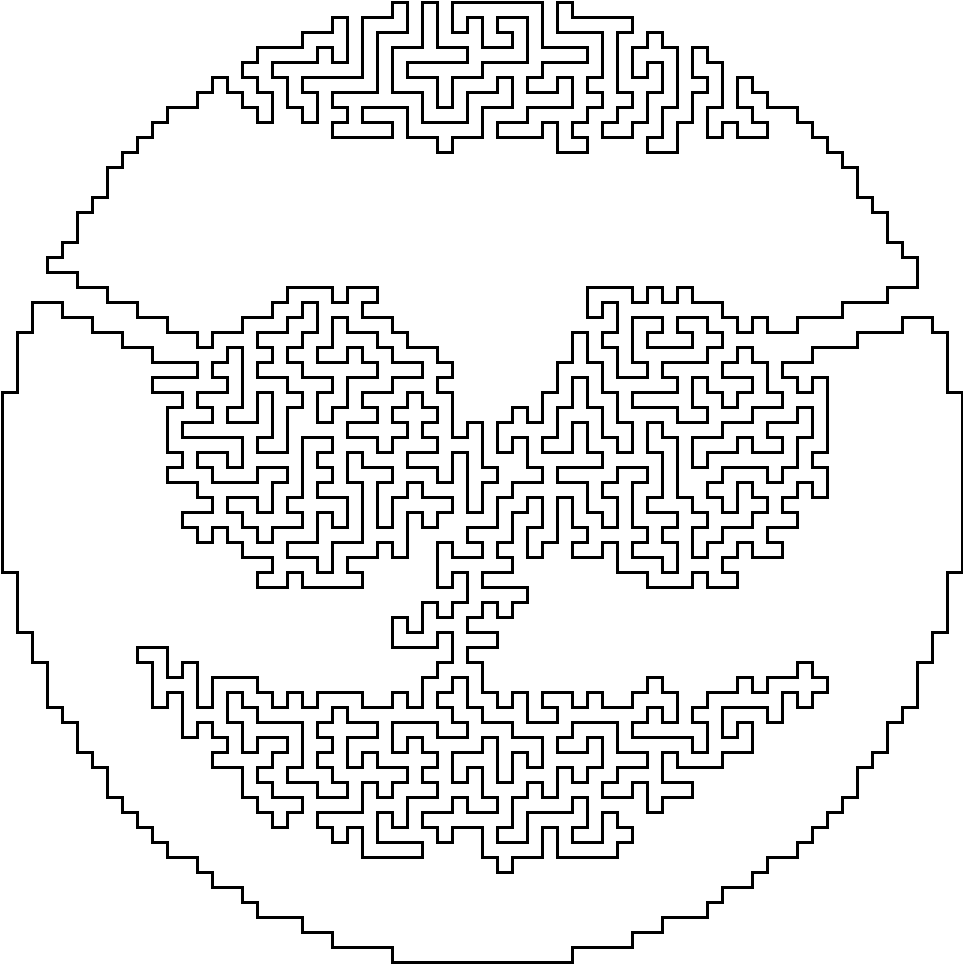
- step1:
利用画图工具将闭合区域填充:

- step2:
用pillow库将图片转为单通道图片并转为矩阵。
from PIL import Image
import numpy as np
path=r"B.png"
im = Image.open(path).convert('L') #三通道转多通道
width = im.size[0] # 获取宽度
height = im.size[1] # 获取高度
im2 = im.resize((int(width*1/15), int(height*1/15)), Image.ANTIALIAS)# 缩小15倍
a=np.array(im2)
np.savetxt("1.txt",a)# 颜色矩阵
得到矩阵后,如果((i,j))处小于等于(128),设置为(1),否则为0,判断((x,y))处是(0)还是(1)即可。
- 学军信友队趣味网络邀请赛
Final standing:

- T1是一道巧妙的构造题。

对于上面的图,输出遍历完所有点的最短时间以及方案,其中最外圈是单向的,箭头所指即为方向,其余对角线之间的道路都是双向的,长度均为1。
可以肯定最短时间是((n cdot (n+1))-1)
对于奇偶我们采用不同的方法讨论,以(n=4)和(n=5)为例。
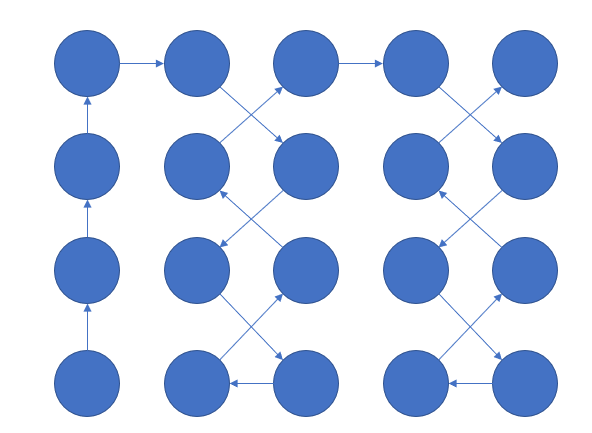
(n=4)的解法
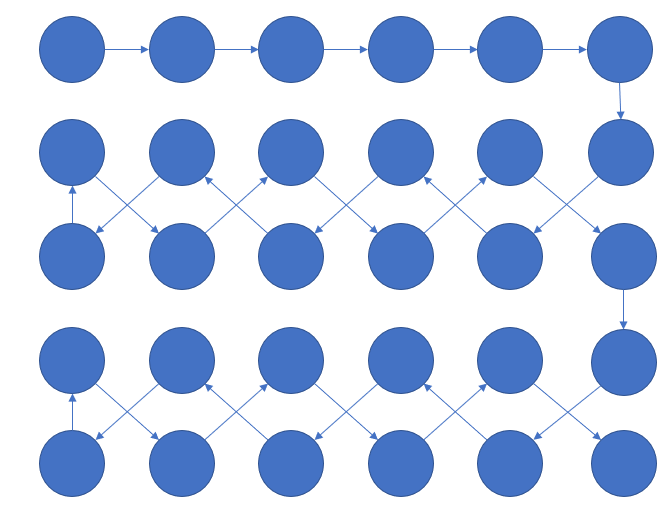
(n=5)的解法
对于(n)为其他数字的情况,和(n=4,5)的构造方法类似,奇偶讨论即可。
/*
* @author: codancer
* @createTime: 2020-04-05, 13:23:23
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
#define pb push_back
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define fep(i,a,b) for(int i=(a);i>=(b);i--)
typedef vector<int> VI;
typedef vector<ll> VII;
typedef pair<int,int> pii;
int main(){
int n;
cin>>n;
cout<<n*(n+1)-1<<endl;
if(n%2==0){
for(int i=n;i>=1;i--) cout<<i<<' '<<1<<endl;
for(int j=2;j<=n+1;j++){
if(j%2==0){
for(int i=1;i<=n;i++){
if(i&1) cout<<i<<' '<<j<<endl;
else cout<<i<<' '<<j+1<<endl;
}
}else{
for(int i=n;i>=1;i--){
if(i&1) cout<<i<<' '<<j<<endl;
else cout<<i<<' '<<j-1<<endl;
}
}
}
}else{
for(int j=1;j<=n+1;j++) cout<<1<<' '<<j<<endl;
for(int i=2;i<=n;i++){
if(i%2==0){
for(int j=n+1;j>=1;j--){
if(j%2==0){
cout<<i<<' '<<j<<endl;
}else{
cout<<i+1<<' '<<j<<endl;
}
}
}else{
for(int j=1;j<=n+1;j++){
if(j&1){
cout<<i-1<<' '<<j<<endl;
}else{
cout<<i<<' '<<j<<endl;
}
}
}
}
}
return 0;
}
- T2是一个常见的的树形dp,即计算一棵树中每个节点所能到达的最远距离。
令(f[i][0])为(i)向下走能走到的最远距离,(f[i][1])是次远距离,同时记录最远距离所经过的子节点,令(f[i][2])代表最终答案,
假设(v)经过了(u)向下走的最大路径,那么(f[v][2]=max(f[u][2],f[u][1])+1),否则(f[v][2]=max(f[u][2],f[u][0])+1)
两次(DFS)转移即可。
/*
* @author: codancer
* @createTime: 2020-04-05, 13:46:51
*/
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
#define pb push_back
#define fi first
#define se second
#define SZ(x) ((int)(x).size())
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define fep(i,a,b) for(int i=(a);i>=(b);i--)
typedef vector<int> VI;
typedef vector<ll> VII;
typedef pair<int,int> pii;
const int N = 300000;
vector<int> G[N];
ll f[N][3];
ll node[N];
bool vis[N];
void dfs(int u,int fa){
for(int v:G[u]){
if(v==fa) continue;
dfs(v,u);
if(f[u][0]<=f[v][0]+1){
f[u][1]=f[u][0];
f[u][0]=f[v][0]+1;
node[u]=v;
}else if(f[u][1]<f[v][0]+1){
f[u][1]=f[v][0]+1;
}
}
}
void dfs2(int u,int fa){
for(int v:G[u]){
if(v==fa) continue;
if(node[u]==v){
f[v][2]=max(f[u][2],f[u][1])+1;
}else{
f[v][2]=max(f[u][2],f[u][0])+1;
}
dfs2(v,u);
}
}
int main(){
int n;
scanf("%d",&n);
vector<ll> w(n+1);
rep(i,1,n){
scanf("%lld",&w[i]);
}
int u,v;
rep(i,1,n-1){
scanf("%d %d",&u,&v);
G[v].pb(u);
G[u].pb(v);
}
dfs(1,-1);
dfs2(1,-1);
ll ans=0;
rep(i,1,n){
ans=max(ans,w[i]*max(f[i][2],f[i][0]));
}
cout<<ans<<endl;
return 0;
}
- 2020算法首届算法竞赛网络挑战赛
Final result:
- 30-Day LeetCoding Challenge
前面的题目较为简单,不再赘述。