Wikipedia definition: “method for solving complex problems by breaking them down into simpler subproblems”,维基的定义看起来和分治算法相似,通过将一个复杂的问题分解成更简单的子问题来进行求解,但是这些子问题相互之间是有联系的,而分治算法定义的子问题之间是无关的,动态规划的两个重要特征:
1、重叠子问题,例如求解斐波那契数,f(n)=f(n-1)+f(n-2)中,f(n-1)和f(n-2)就有很多重叠子问题,其实f(n-1)包含了f(n-2),整个f(n-2)都是其重叠子问题
2、最优子结构,在求解问题的最优解时,需要构建问题的最优解结构,如果这个问题的解结构包含子问题的最优解,则称该问题具有最优子结构。
动态规划问题的解题步骤:
1、定义子问题(Define subproblems)
2、记录重复出现的子问题(Write down the recurrence that relates subproblems),构造解方程
3、识别并计算基本状态(Recognize and solve the base cases)
动态规划问题示例:
1、数的组和问题
给定一个数n,计算有多少种方式可以作为1,3,4的和,也就是1,3,4有多少种组和方式其和的结果为n。求解过程如下:
a 定义子问题
设D(n)为数字1,3,4组和后和为n的不同方法数
b 构造解方程
假设n=x1+x2+.....+xm;如果xm=1,则剩下的数据之和为n-1,设D(n-1)为1,3,4不同组和的方法数;同理,如果xm=3,则D(n-3)为1,3,4不同组和为n-3的方法数,同理D(n-4);因为xm可能为1,3,4,所以D(n)=D(n-1)+D(n-3)+D(n-4)
c 计算基本情况解,定义基本问题解
D(0)=1,如果n<0,则D(n)=0,同理可知:D(0)=D(1)=D(2)=1,D(3)=2(3=3,3=1+1+1 两种情况);以上定义完毕,根据以上描述,可以定义程序结构:
def sumToN(n):
if(n<=2);
return 1;
if(n==3):
return 2;
D[0]=D[1]=D[2]=1;
D[3]=2;
for(i=4;i<=n;i++):
D[i]=D[i-1]+D[i-3]+D[i-4];
return D[n];
2、钢条切割最大收益问题
《算法导论》中动态规划第一个示例章节中的问题,钢条的长度和价格对应关系用下图来表示,给定一个长度n的钢条,如何切割才能使其价值最大?

猛地一下就去找最优结构然后构造最优解的结构太难了,先从简单入手,给定长度i,对应的最大收益r(i)可以从以下计算进行递推:
i=1,r(i)=1;i=1时,只有这一种情况
i=2,r(i)=?,需要分析了,如果进行切割了,则r(i)=r(1)+r(1),如果不进行切割,r(i)=5,显然前者r(i)=2,取较大者,r(i)=5
i=3,r(i)=?,同样,如果进行切割了,第一次切割可能是1,也可能是2,所以r(i)=max{r(1)+r(2),r(2)+r(1)}=6,显然这个计算是有重叠的,如果不切割, r(i)=8,取较大者,r(i)=8
i=4,r(i)=?,用同样的方法进行分析,则r(i)=max{r(1)+r(3),r(2)+r(2),r(3)+r(1),p(i)},其中p(i)表示不切割时的价格
由此,可以更一般地得出结论,对于长度n的钢条,其收益情况如下:
r(n)=max{p(n),r(1)+r(n-1),r(2)+r(n-2),r(3)+r(n-3),....,r(n-1)+r(1)}
这是一种描述方法,还有一种更加简单的描述方法:对于r(n),所有的价值组成有:
不切割,直接返回p(n)
先切割长度为1,剩下n-1的用相同的方法继续求解,此时返回p(1)+r(n-1)
先切割长度为2,剩下n-2的用相同的方法继续求解,此时返回p(2)+r(n-2)
....
取最大值,可以得出:r(n)=max{p(i)+r(n-i)},其中1<=i<=n
此时,可以设计一个自顶向下的方法进行求解:
cud-rod(p,n):
if n==0 return 0
q=-1
for i=1 to n:
q = max(q,p[i]+cud-rod(p,n-i)
return q
这个递归是有严重的重复计算的,f(n)=max{p(i)+f(n-i)},f(n)需要计算从f(1)到f(n-1),f(n-1)需要计算从f(1)到f(n-2).....
为了不重复计算,可以用备忘机制,自底向上的备忘模式如下:
memoized-cut-rod(p,n):
r[n]={-1,-1,...}// create a array with n's -1
return memoized-cut-rod-aux(p,n,r)
memoized-cut-rod-aux(p,n,r):
if r[n]>-1
return r[n];// the value has been calculated already
if n==0
q=0
else q=-1
for i=1 to n:
q=max(q,p[i]+memoized-cut-rod-aux(p,n-i,r))
r[n]=q;// store the calculated result
return q; //return the result
自顶向下的计算是使用倒推的方法进行的,符合递归定义
自底向上版本则更为简单:
bottom-up-cut-rod(p,n):
r[n]={-1,-1,....};//create an array
r[0]=0; //set initial value
for j = 1 to n:
q=-1
for i=1 to j:
q=max(q,p[i]+r[j-i])
r[j]=q
return r[n]
上述方法返回了最大价值的结果,但是并没有记录切割方法,所以还需要进行切割方法的记录,可以扩展自底向上版本方法:
extended-bottom-up-cut-rod(p,n):
r[n]={-1,-1,.....} //用于记录价值
s[n]={-1,-1,.....} //用于记录切割长度
r[0]=0
for j=1 to n
q= -1
for i=1 to j
if q < p[i]+r[j-i]
q=p[i]+r[j-i]
s[j]=i
r[j]=q
return r and s
然后就是打印最优解:
print-cut-rod-solution(p,n):
r,s = extended-bottom-up-cut-rod(p,n);
while n>0:
print(s[n])
n=n-s[n]
3、多米诺骨牌组和问题,http://poj.org/problem?id=2663,3*n的矩形,需要用2*1的长方形进行组和,求组和方式,这是一种3*12的组和:

当n=2,也就是前两个位置的组和方式有3种,故而剩下的摆放方法的种类有3*f(n-2)中
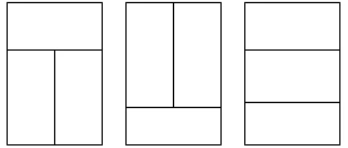
当n=4,出去n=2的组和,组和方式有2种:


注意这里,n=4时,除了用n=2的组和方式之外(f(n-2)已经包含了),还有上述图中的两种,故而剩下的摆放方法有2*f(n-4)种,
同理可以得知f(n-6),f(n-8)....也是两倍的关系,递推方程为:
f(2)=3
f(4)=3*f(2)+2*1
f(6)=3*f(4)+2{f(2)+1}
f(n)=3*f(n-2)+2{f(n-4)+...+f(0)},其中f(0)=1
简化方程可以得出:f(n)=4*f(n-2)-f(n-4);根据方程进行程序设计:
combinations(n):
if n % 2 != 0 return 0;
if n==0 return 1;
if n==2 return 3;
return 4*combinations(n-2)-combinations(n-4);
上述方法存在重复计算,可以使用记录法简化计算:
combinations-aux(n):
p[n]={-1,-1,...};
combinations-memo(n,p);
return p[n];
combinations-memo(n,p):
if(n==0) p[n]=1;
if(n==2) p[n]=3;
if(p[n]!=-1) return p[n];
p[n]=4*combinations-memo(n-2,p)-combinations-memo(n-4,p);
return p[n];
因为已经有了递推公式,所以可以用自底向上的方法求解:
bottom-up-combinations(n):
p[n]={}
p[0]=1
p[2]=3
for i= 4 to n:
p[i]=4*p[i-2]-p[i-4];
i+=2
return p[n]
自底向上的求解好像更加简单了......