题目链接:https://codeforces.com/contest/1245/problem/D
题目大意:
平面上有n座城市,第i座城市的坐标是 (x[i], y[i]) ,
你现在要给n城市供电,对于第i座城市,你可以选择两种方式给其供电:
- 建造一个发电站供电,这需要花费 (c[i]) ;
- 连一条连向城市j的电缆,这需要花费 ((|x[i]-x[j]|+|y[i]-y[j]|) imes (k[i]+k[j])) 。
现在告诉你n以及 (x[i], y[i], c[i], k[i]) ,请你求出以下信息:
- 最少花费;
- 自己发电的城市数量;
- 自己发电的城市编号;
- 城市间连接电缆的数量;
- 所有连接有电缆的城市对。
解析思路:
这道题目就是一道最小生成树裸题。
首先,除了 (n) 个节点以外,我再开一个点 (S)(在我的程序中 (S = 0)),然后将 (n) 个点中的任意一点 (i) 分别向 (S) 连一条权值为 (c[i]) 的边,
(n) 个点两两之间(设两点编号为 (i) 和 (j))连一条权值为 ((|x[i]-x[j]| + |y[i]-y[j]|) imes (k[i]+k[j])) 的边。
然后求这 (n+1) 个点的最小生成树。
整个图大致如下:
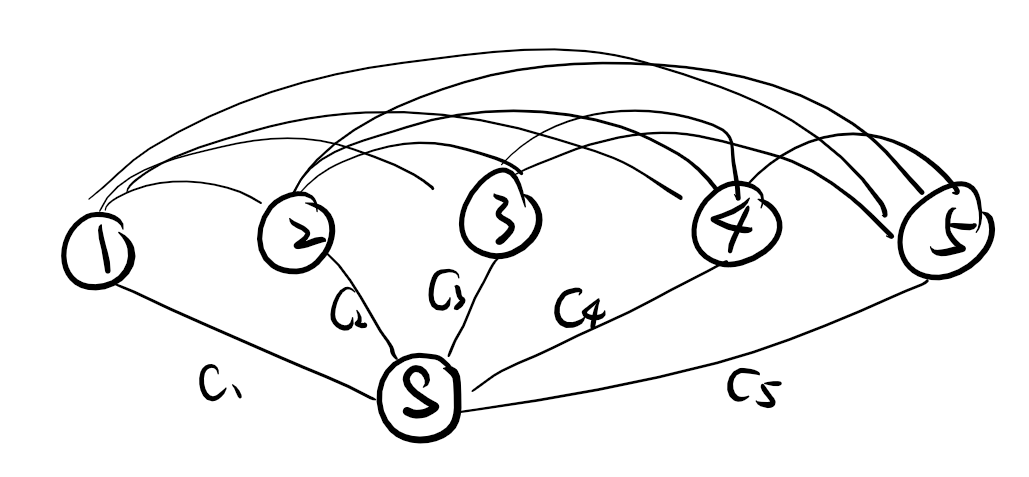
然后在最小生成树的 (n) 条边中,如果这条边的一个端点是 (S) ,那么另一个端点 (i) 就是自己建站的;
否则,这条边上的两点就是有连接关系的。
这样就能得到题目所要求的所有数据。
实现最小生成树可以使用kruskal或者prim算法,我这里使用kruskal实现。
实现代码如下:
#include <bits/stdc++.h>
using namespace std;
#define INF (1<<29)
const int maxn = 2020, maxm = 5000500;
struct Edge {
int u, v;
long long w;
Edge() {}
Edge(int _u, int _v, long long _w) { u = _u; v = _v; w = _w; }
} edge[maxm];
long long x[maxn], y[maxn], c[maxn], k[maxn], cost[maxn];
int n, cnt, f[maxn];
vector<int> res1;
vector<pair<int, int> > res2;
bool cmp(Edge a, Edge b) { return a.w < b.w; }
void init() {
for (int i = 0; i <= n; i ++) f[i] = i;
}
int func_find(int x) {
return x == f[x] ? x : f[x] = func_find(f[x]);
}
void func_union(int x, int y) {
int a = func_find(x), b = func_find(y);
f[a] = f[b] = f[x] = f[y] = min(a, b);
}
void kruskal() {
init();
sort(edge, edge+cnt, cmp);
int cc = 0;
long long ans = 0LL;
for (int i = 0; i < cnt; i ++) {
int u = edge[i].u, v = edge[i].v;
long long w = edge[i].w;
// printf("u = %d , v = %d , w = %lld
", u, v, w);
if (func_find(u) != func_find(v)) {
ans += w;
cc ++;
if (!u) res1.push_back(v);
else if (!v) res1.push_back(u);
else res2.push_back(make_pair(u, v));
func_union(u, v);
if (cc == n) break;
}
}
cout << ans << endl;
}
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> x[i] >> y[i];
for (int i = 1; i <= n; i ++) cin >> c[i];
for (int i = 1; i <= n; i ++) cin >> k[i];
for (int i = 1; i <= n; i ++) edge[cnt++] = Edge(0, i, c[i]);
for (int i = 1; i <= n; i ++) for (int j = 1; j <= n; j ++) edge[cnt++] = Edge(i, j, (abs(x[i]-x[j])+abs(y[i]-y[j]))*(k[i]+k[j]));
kruskal();
int sz = res1.size();
cout << sz << endl;
for (int i = 0; i < sz; i ++) {
if (i) putchar(' ');
cout << res1[i];
}
cout << endl;
sz = res2.size();
cout << sz << endl;
for (int i = 0; i < sz; i ++) {
cout << res2[i].first << " " << res2[i].second << endl;
}
return 0;
}