原题链接:http://ac.jobdu.com/problem.php?pid=1113
- 题目描述:
-
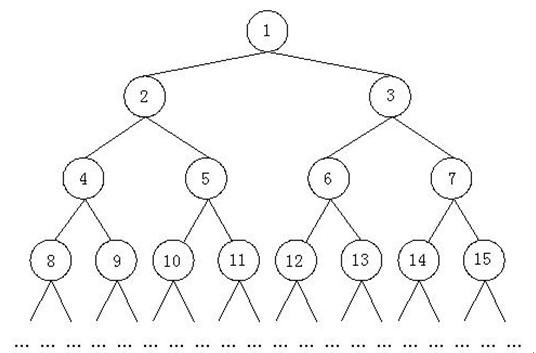
如上所示,由正整数1,2,3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是,结点m所在的子树中一共包括多少个结点。
比如,n = 12,m = 3那么上图中的结点13,14,15以及后面的结点都是不存在的,结点m所在子树中包括的结点有3,6,7,12,因此结点m的所在子树中共有4个结点。
- 输入:
-
输入数据包括多行,每行给出一组测试数据,包括两个整数m,n (1 <= m <= n <= 1000000000)。最后一组测试数据中包括两个0,表示输入的结束,这组数据不用处理。
- 输出:
-
对于每一组测试数据,输出一行,该行包含一个整数,给出结点m所在子树中包括的结点的数目。
- 样例输入:
-
3 12 0 0
- 样例输出:
- 4
- 题解:
- 递归版本:
- 这道题第一想法是递归,左子树和右子树的结点数和再加1。
- 代码如下:

1 #include <stdio.h> 2 3 int nodeNum_rec(int m,int n) 4 { 5 if(m>n) 6 return 0; 7 return nodeNum_rec(2*m,n)+nodeNum_rec(2*m+1,n)+1; 8 } 9 int main() 10 { 11 int n,m; 12 int num; 13 14 freopen("tree.in","r",stdin); 15 freopen("tree.out","w",stdout); 16 17 while(scanf("%d %d",&m,&n)!=EOF&&m&&n) 18 { 19 20 num=nodeNum_rec(m,n); 21 22 printf("%d ",num); 23 } 24 25 return 0; 26 }
当题目中n的数目到达十亿级别是,显然这么做会超时的。
非递归版本:
这道题的另一种解法是采用非递归,即利用完全二叉树的性质,倒数第二层网上必定是满二叉树,先计算满二叉子树的结点数,然后再根据情况加上剩下的部分。代码如下:

1 #include <stdio.h> 2 #include <math.h> 3 int nodeNum(int m,int n) 4 { 5 int deep_n,deep_m; 6 int sum; 7 int k; 8 int start,end; 9 10 deep_n=log(n)/log(2)+1;//n的高度 11 deep_m=log(m)/log(2)+1;//m的高度 12 sum=0; 13 k=1; 14 //计算到倒数第二层,这几层肯定都是满的,且是按照1、2、4的规律 15 for(int i=0;i<deep_n-deep_m;i++){ 16 sum=sum+k; 17 k=2*k; 18 } 19 20 //计算m的子树在最后一层的起始点和最后节点 21 start=m*k; 22 end=start+k; 23 if(end<=n)//最后一层也是满的 24 sum=sum+k; 25 else//最后一层不是满的,还差多少补上 26 { 27 28 for(int i=start; i<=n; i++) 29 { 30 sum++; 31 } 32 33 } 34 return sum; 35 } 36 37 int main() 38 { 39 int n,m; 40 int num; 41 42 freopen("tree.in","r",stdin); 43 freopen("tree.out","w",stdout); 44 45 while(scanf("%d %d",&m,&n)!=EOF&&m&&n) 46 { 47 48 num=nodeNum_rec(m,n); 49 50 printf("%d ",num); 51 } 52 53 return 0; 54 }
