力扣上也有一道类似的题 几乎是一样 输出不同 → 力扣leetcode 435. 无重叠区间
区间贪心是比较经典的 就拿洛谷P1803来举例
题目大意
n个比赛 [开始时间,结束时间] 问一个人最多能参加几个(不能同时参加两个且必须有始有终)

题解
首先考虑最简单的情况,如果区间L1被区间L2包含(图a),那么显然选择L1是最好的,也符合局部贪心思想。
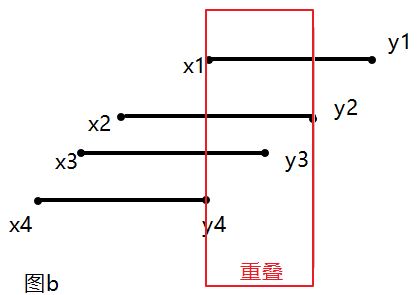
然后把所有区间按左端点(此例子就是开始时间)从大到小排序,如果把重叠的区间去除了,必然得到的是y1>y2>...>yn(图b)
所以选择的时候,以y1为第一个选择的,去除重叠部分后,下一个只能选择y4,因此总是选择端点最大的区间进行比较可以是左端点从大到小排序,也可以是从右端点开始

Show me the code
#include <bits/stdc++.h> //万能头文件
using namespace std;
const int maxn = 1000000;
struct inteval{
int s, e; //开始s 结束e
}I[maxn];
bool cmp(inteval a, inteval b){
if(a.s != b.s) return a.s > b.s; // 先按开始时间从大到小排序
else return a.e < b.e; // 开始时间相同时按结束时间从小到大排序
}
int main(){
int n;
cin >> n;
for (int i = 0; i < n; i++)
cin >> I[i].s >> I[i].e ;
sort(I, I + n, cmp); // 区间排序
// ans 记录不相交区间 也就是能同时得到的区间
// lastS 记录上一个选中区间的开始端点
int ans = 1, lastS = I[0].s;
for (int i = 1; i < n; i++){
if(I[i].e <= lastS){ // 如果该区间的右端点(结束时间)在lastS左边
lastS = I[i].s; // 以I[i] 作为新选中的区间
ans ++; // 不想交数 ++
}
}
cout << ans;
return 0;
}