公号:码农充电站pro
主页:https://codeshellme.github.io
计算机最基本的工作是处理数据,而数据的最底层表现形式是二进制,并非是我们人类熟悉的十进制。可以这么认为,计算机其实是很“笨的”,它只理解二进制数据。
今天,主要介绍计算机是怎样做加减运算的。你可能会想,加减运算?这么简单的事情,还用介绍?也许还真不是你想的那样。
计算机的运算是由CPU 完成的,而CPU 只会做加法运算,不会做减法运算,那计算机怎样完成减法工作呢?
1,二进制数
我们先来看看二进制数。
二进制数是由0,1 组成的,比如:
- 十进制的5,用二进制表示是 101。
- 十进制的7,用二进制表示是 111。
数字由正数和负数组成。为了表示正负数,计算机中就有了有符号数和无符号数之分:
- 无符号数:英文为
unsigned,只能表示正数。 - 有符号数:英文为
signed,即能表示正数,又能表示负数。
C/C++ 语言中的数字有有符号数和无符号数之分。
Java 语言所有的数字都是有符号数。
假如,我们用 4 位二进制,来表示无符号数,也就是只表示正数,能表示的范围是 0 到 15,转换关系如下表:
| 十进制数 | 二进制数 | 十进制数 | 二进制数 |
|---|---|---|---|
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | 10 | 1010 |
| 3 | 0011 | 11 | 1011 |
| 4 | 0100 | 12 | 1100 |
| 5 | 0101 | 13 | 1101 |
| 6 | 0110 | 14 | 1110 |
| 7 | 0111 | 15 | 1111 |
有符号数,即要表示正数,也要表示负数。
要用二进制表示有符号数,需要用二进制的最高位来表示符号,0 表示正,1 表示负。所谓的最高位,也就是最左边那一位。
用 4 位二进制,来表示有符号数,能表示的范围是 -8 到 7,转换关系如下表:
| 十进制数 | 二进制数 | 十进制数 | 二进制数 |
|---|---|---|---|
| 0 | 0000 |
-8 | 1000 |
| 1 | 0001 |
-1 | 1001 |
| 2 | 0010 |
-2 | 1010 |
| 3 | 0011 |
-3 | 1011 |
| 4 | 0100 |
-4 | 1100 |
| 5 | 0101 |
-5 | 1101 |
| 6 | 0110 |
-6 | 1110 |
| 7 | 0111 |
-7 | 1111 |
上表中的最高位的符号位,已标红。
要注意,对于有符号的4 位二进制 ----
1000不是-0,而是-8。
可以总结出,对于N 位的二进制数:
- 无论是表示有符号数还是无符号数,都能表示
2^N个数字。 - 若用于表示无符号数,则能表示的范围是
[0, 2^N - 1]。 - 若用于表示有符号数,则能表示的范围是
[-2^(N-1), 2^(N-1) - 1]。- 需要注意,在有符号数中,对于符号位是
1,后面N-1位全是0,这种情况表示的是-2^(N-1)(也就是所能表示的最小值),而不是-0。 - 实际上是将
-0这种情况解释成了最小值,否则就会出现+0和-0两个0。
- 需要注意,在有符号数中,对于符号位是
2,二进制原码
上面介绍到的二进制就是原码形式。
原码就是除符号位外的其他位,保存该二进制数的绝对值。
用原码进行加法计算
计算机中的数字运算都会先转成二进制数再进行计算。
我们用原码来计算加法,用4 位二进制数来计算 3 + 2,过程如下:
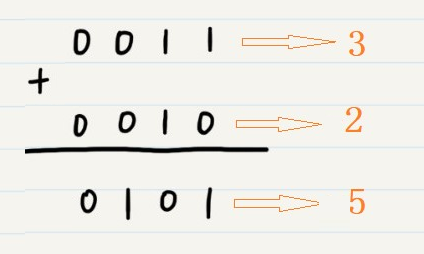
可以看到,用原码计算加法是没有问题的。
用原码进行减法计算
我们再用原码来计算减法,因为CPU 只会计算加法,所以计算减法时,会将减法转换成加法。
比如,用4 位二进制数来计算计算 3 - 2,会将其转换成 3 + (-2), 过程如下:

可以看到 3-2 计算出来的结果是 -5,显然是错误的。
所以,用二进制原码来计算减法是行不通的。实际上,计算机计算减法用的是补码。
在介绍补码之前,我们先来看下什么是溢出。
3,数字溢出
计算机中数字的表示是需要内存空间的,不同类型的数字所能占用的空间是不一样的。
比如,在Java 语言中short 类型占用 2 个字节,int 类型占用 4 个字节。
一个字节等于 8 位。
既然空间大小是有限制的,所以计算机中的数字也是有范围的,即上限和下限,如果数字超出限制,就会产生溢出。超出上限叫上溢出,超出下限叫下溢出。而溢出的部分会直接被舍去。
就像我们在上文中介绍的,对于N 位二进制有符号整数,所能表示的范围是 [-2^(N-1), 2^(N-1) - 1]。
由于溢出的部分会被舍去,那么最大值加1,将发生上溢出,变为最小值;最小值减1,将发生下溢出,变为最大值。
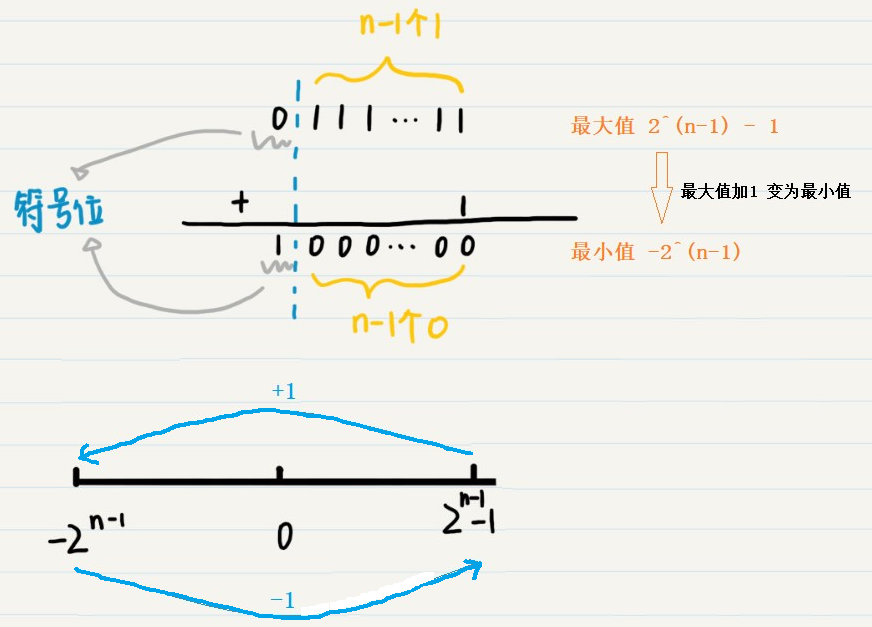
我们用Java 中的int 类型来验证,Java 中int 类型的最大、最小值分别是:
- 最大值:
Integer.MAX_VALUE,是2147483647。 - 最小值:
Integer.MIN_VALUE,是-2147483648。
用下面代码验证:
System.out.println(Integer.MAX_VALUE + 1 == Integer.MIN_VALUE); // true
System.out.println(Integer.MIN_VALUE - 1 == Integer.MAX_VALUE); // true
这两行代码的输出均为true,说明最大值加1 变为最小值,最小值减1 变为最大值。
所以,在计算机中,只要一个整数的类型确定了,那么它所能占用的内存空间大小也就确定了,从而它所能表示的数字范围也就确定了。那么不管给这个整数加多大的数字,或者减多大的数字,最终的结果都只能在这个范围内旋转。
就像表盘一样,当表针走过最大值的时候,就变成了最小值。

同样,这也等同于数学中的取余运算。只要分母确定了,不管分子是多大,或者多小的数字,最终的结果也都是在一个确定的范围之内。
比如我们对十进制5 进行取余计算,那么最终的结果都是在[0, 4] 范围之内,如下:
0 % 5 = 02 % 5 = 2397 % 5 = 299999 % 5 = 4
可以总结出,对数字N 进行取余,N >= 2 且为整数,那么结果都在 [0, N-1] 范围之内。
4,二进制反码与补码
知道了溢出,就可以介绍CPU 如何计算减法了。CPU 的减法运算使用了二进制补码,补码实际上就是采用了溢出的原理。
我们直接给出反码与补码的定义:
- 反码定义:正数的反码等于其原码,负数的反码是其原码除符号位外,按位取反。
- 补码定义:正数的补码等于其原码,负数的补码是其反码加1。
比如下面的几个数字:
| 十进制数 | 2 | 3 | -2 | -5 |
|---|---|---|---|---|
| 二进制原码 | 0010 | 0011 | 1010 |
1101 |
| 二进制反码 | 0010 | 0011 | 1101 |
1010 |
| 二进制补码 | 0010 | 0011 | 1110 |
1011 |
我们用4 位二进制补码来计算 3+(-2),如下:
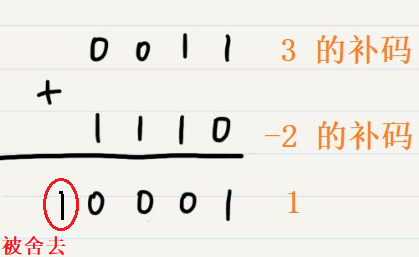
最高位的1 发生上溢出,直接被舍去,所以结果是正确的。
所以,要记住,真实的计算机中的二进制是用补码表示的,而不是原码。
5,总结
本篇文章主要介绍了:
- CPU 只能做加法,不能做减法,减法要转成加法做计算。
- 二进制数字有三种表示方式:
- 原码:除符号位外的其他位,保存该二进制数的绝对值。
- 反码:正数的反码等于其原码,负数的反码是其原码除符号位外,按位取反。
- 补码:正数的补码等于其原码,负数的补码是其反码加1。
- 计算机中的数字采用二进制补码表示,而不是原码表示。
- 补码采用了溢出的原理。
- 计算机中的数字是有范围限制的,超出限制会发生溢出。
- 超出上限叫做上溢出。最大值加1会发生上溢出,变为最小值。
- 超出下限叫做下溢出。最小值减1会发生下溢出,变为最大值。
(本节完。)
推荐阅读:
欢迎关注作者公众号,获取更多技术干货。
