公号:码农充电站pro
主页:https://codeshellme.github.io
线性回归模型用于处理回归问题,也就是预测连续型数值。线性回归模型是最基础的一种回归模型,理解起来也很容易,我们从解方程组谈起。
1,解方程组
相信大家对解方程都不陌生,这是我们初中时期最熟悉的数学知识。
假如我们有以下方程组:
- 2x + y = 3 —— ①
- 5x - 2y = 7 —— ②
要解上面这个方程组,我们可以将第一个方程的等号两边都乘以2:
- 4x + 2y = 6 —— ③
再将第2 个方程与第3 个方程的等号两边分别相加:
- 9x = 13 —— ④
这样我们就将变量y 消去了,就可以求解出x 的值。然后再将x 的值代入第1或第2个方程中,就可以解出y 的值。
以上这个解方程的过程就是高斯消元法。
2,线性回归模型
如果将上面方程组中的任意一个表达式单拿出来,那么x 和 y 都是一种线性关系,比如:
- y = 3 - 2x
该表达式中,我们将x 叫做自变量,y 叫作因变量。
如果将其扩展到机器学习中,那么特征集就相当于自变量X,目标集就相当于因变量Y。
当自变量的个数大于1时,就是多元回归;当因变量的个数大于1 时,就是多重回归。
线性回归模型的目的就是想找出一种特征集与目标集之间的线性关系,使得我们可以通过已知的特征数据预测出目标数据。
通常,我们的模型是通过多个特征值来预测一个目标值,那么线性回归模型的数学公式为:
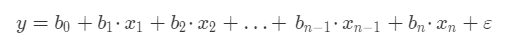
其中:
- y 表示我们要预测的目标值。
- x1,x2...xn 代表每个特征,一共有n 个特征。
- b1,b2...bn 代表每个特征的系数,特征系数也代表了某个特征对目标值的影响。
- b0 是一个常数,称为截距。
- ε 表示模型的误差,也被称作损失函数。
线性回归模型与数学中的解方程不同,后者的结果是精确解,而前者则是一个近似解。因此在公式中存在一个 ε 。
我们的目标是求得一组使得 ε 最小的特征系数(b1,b2...bn),当有了新的特征时,就可以根据特征系数求得预测值。
回归一词的来源
1875 年,英国科学家弗朗西·斯高尔顿(达尔文的表弟)尝试寻找父代身高与子代身高之间的关系。
在经过了1078 份数据的分析之后,最终他得出结论:人类的身高维持在相对稳定的状态,他称之为回归效应,并给出了历史上第一个回归公式:
Y = 0.516X + 33.73
公式中的 Y 代表子代身高,X 代表父代身高,单位为英寸。
3,线性拟合
线性拟合中不存在精确解,但是存在最优解,也就是使得 ε 最小的解。
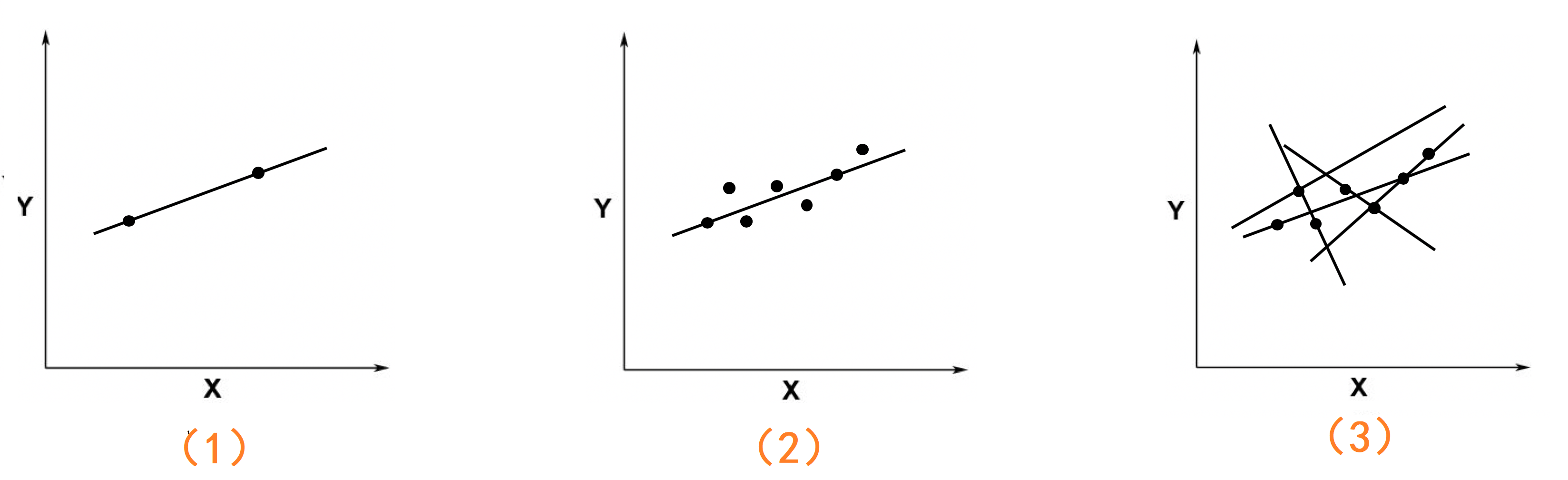
上图中有3 个坐标系:
- 在第1个图中只有两个点,这时候存在一条唯一的直线能够同时穿过这两个点,这条直线就是精确解。
- 当坐标中的点多于两个时,比如第2个图,这时候就不可能存在一条直线,同时穿过这些点。但是会存在多条直线,会尽可能多的穿过更多的点,就像图3。而这些直线中会有一条直线,是这些点的最好的拟合。
如何才能找到这条最好的拟合的直线呢?
4,最小二乘法
最小二乘法可以用来求解这个最优直线。
最小二乘法的主要思想是让真实值与预测值之差(即误差)的平方和达到最小。用公式表示如下:
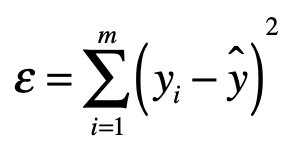
上面的公式中:
- yi 是数据的真实值。
- y^ 是数据的预测值。
- ε 是我们要找的最小误差,它是所有的真实值与预测值之差的平方的和。
方程组除了可以使用高斯消元法求解之外,还可以使用矩阵来求解。
将上面的 ε 公式写成矩阵的形式就是:
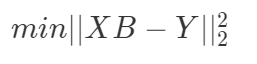
其中:
- B 为系数矩阵
- X 为特征矩阵
- Y 为目标矩阵
我们的目标就是找到一个向量B,使得向量 XB 与 Y 之间欧氏距离的平方数最小。
经过一系列的推导之后,系数矩阵B 为:
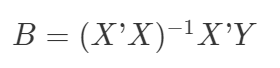
其中:
X'是X的转置矩阵。(X'X)-1 是(X'X)的逆矩阵。
5,用 numpy 库进行矩阵运算

NumPy 是一个使用Python 进行科学计算的软件包,其中就实现了我们需要的矩阵运算:
x.transpose():矩阵x 的转置运算。x.dot(y):矩阵x 点乘矩阵y。x.I:返回可逆矩阵x 的逆矩阵。
那么根据公式:
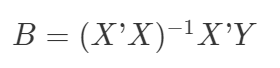
我们可以编写求B 的函数:
def get_B(X, Y):
_X = X.transpose()
B = (_X.dot(X)).I.dot(_X).dot(Y)
return B
假设我们有以下数据集,要对该数据集进行线性拟合:
| 特征x1 | 特征x2 | 目标y |
|---|---|---|
| 0 | 1 | 1.4 |
| 1 | -1 | -0.48 |
| 2 | 8 | 13.2 |
我们知道线性回归的公式为:
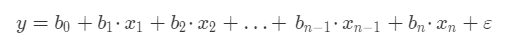
那么上面表格的数据转化为方程组:
- b0 + b1⋅0 + b2⋅1 = 1.4
- b0 + b1⋅1 - b2⋅1 = −0.48
- b0 + b1⋅2 + b2⋅8 = 13.2
那么矩阵X 为:
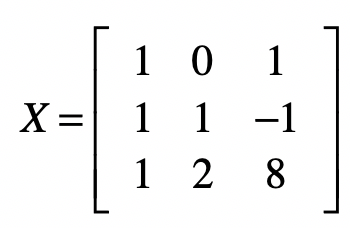
转化为代码如下:
from numpy import *
X = mat([
[1,0,1],
[1,1,-1],
[1,2,8]
])
Y = mat([[1.4],[-0.48],[13.2]])
计算系数矩阵B:
>>> get_B(X, Y)
matrix([[-0.01454545], # b0
[ 0.94909091], # b1
[ 1.41454545]]) # b2
这样就得出了各个系数项,我们可以用这些系数项进行数据预测。
6,sklearn 对线性回归的实现
sklearn 库中的 LinearRegression 类是对线性回归的实现。
LinearRegression 类的原型:
LinearRegression(
fit_intercept=True,
normalize=False,
copy_X=True,
n_jobs=None)
来看下其参数的含义:
- fit_intercept:拟合模型时,是否存在截距
b0,默认为True,即存在。 - normalize:在拟合模型之前,是否要对特征集进行标准化处理。
- 当 fit_intercept 为
False时,该参数被忽略。
- 当 fit_intercept 为
- copy_X:是否复制特征集
X。 - n_jobs:用于计算的作业数,只对多重回归且比较复杂的数据进行加速。
接下来,使用 LinearRegression 类对上面表格数据进行拟合。(为了方便查看,我将表格放在这里)
| 特征x1 | 特征x2 | 目标y |
|---|---|---|
| 0 | 1 | 1.4 |
| 1 | -1 | -0.48 |
| 2 | 8 | 13.2 |
将该表格数据转化成 Python 变量,如下:
X = [(0, 1), [1, -1], [2, 8]]
Y = [1.4, -0.48, 13.2]
创建线性回归对象:
from sklearn.linear_model import LinearRegression
reg = LinearRegression() # 均使用默认参数
拟合数据:
reg.fit(X, Y)
coef_ 属性是特征系数列表:
>>> reg.coef_
array([0.94909091, 1.41454545])
intercept_ 属性是截距 b0 的值:
>>> reg.intercept_
-0.014545454545452863
通过coef_ 和intercept_ 属性可以看到,使用 LinearRegression 类和使用 NumPy 得到的结果是一样的。
需要注意的是,只有当数据集的特征集与目标集是线性关系时,才能使用线性回归拟合出一个不错的结果。如果不是线性关系,则拟合结果一般不会很好。
对于非线性关系的回归问题,可以使用树回归等其它模型。
那如何判断特征集与目标集是否是线性关系呢?有两个指标:
- 决定系数 R2:该指标使用了回归平方和与总平方和之比,是反映模型拟合度的重要指标。
- 它的取值在 0 到 1 之间,越接近于 1 表示拟合的程度越好、数据分布越接近线性关系。
- 校正的决定系数 Rc2:如果特征非常多,那么Rc2 指标将更加可靠。
LinearRegression 类中的 score 方法就是R2 指标的实现:
>>> reg.score(X, Y)
1.0 # 结果是 1,说明特征集与目标集是非常好的线性关系。
7,对波士顿房价进行线性分析
对于波士顿房价数据集,之前的文章中,已经多次使用过,这次我们对其使用线性回归模型进行分析。
首先加载数据:
from sklearn.datasets import load_boston
boston = load_boston()
features = boston.data # 特征集
prices = boston.target # 目标集
创建线性回归对象:
from sklearn.linear_model import LinearRegression
# 在拟合之前对数据进行标准化处理
reg = LinearRegression(normalize=True)
拟合数据:
reg.fit(features, prices)
对模型进行评分:
>>> reg.score(features, prices)
0.7406426641094095
通过评分可知,最终的准确率为74.1%,虽谈不上很高,但也还说得过去。
8,总结
使用最小二乘法训练出的线性回归模型是最简单基础的一种线性模型,只有当特征集与目标集呈线性关系时,它才能拟合出比较好的结果。
在它的基础之上,还有很多改进版的线性模型,比如:局部加权线性回归,岭回归,lasso 等,你可以在 Sklearn Linear Models 进一步了解和学习。
(本节完。)
推荐阅读:
欢迎关注作者公众号,获取更多技术干货。
