作为一名程序猿,假如某一天,有一个妹子拿着一个浮点数,求你教她怎么换算成二进制,如果你不能单手求出来,你都不能算一个合格的工具人.....好吧,是一个合格的程序猿(狗头保命)。

回归正题,有好多小伙伴去工作之后,早已经忘了最基本的计算机基础,今天,来讲下,在计算机中,怎么用二进制表示浮点数?下次再有人问你,就把这篇文章丢给他。
作为一种数据类型,浮点数应用广泛。在处理诸如订单交易、货币计算、或者商品金额的方面,应该小心慎用浮点数。在定义浮点数变量的时候,不完全理解原理,就容易出现各种揪心的问题。
那么,正题来了。
浮点数在计算机中的存储方式遵循IEEE 754浮点数的计数标准,那么,IEEE 754浮点数的计数标准怎么表示浮点数的?
- 浮点数数学表示:
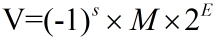
- 符号位(sign):决定该浮点数的正负
- 尾数(significand):二进制小数,范围在[1,2)或者[0,1)中
- 阶码(exponent):对浮点数加权,权重为2的E次幂
IEEE标准754规定了三种浮点数格式:单精度、双精度、扩展精度。前两者正好对应C语言里头的float、double,限于篇幅,本文仅讨论单精度、双精度浮点格式。
其实,IEEE754标准可以概括成一张图片,如下

采用尾数+阶码的编码方式。其实就是在我们学过的数学知识中,就是类似于科学计数法。即有效数字+指数位。
所以,只要给出:符号(S)、尾数部分(M)、阶码部分这三种信息,就可以正确的表示一个浮点数。在C语言中,浮点数的数据类型最常用的就是float、double,那么,他们在计算机中的存储结构是怎样的呢?


浮点数的各个部分的含义如下表格所示
| 符号部分(S) | 阶码部分(E) | 尾数部分(M) |
|---|---|---|
| 0表示正(+),1表示负(-) | 阶码部分其实就是指数部分 float 指数部分8位,可以表示的指数范围位-127~128 double 指数部分11位,可以表示的指数范围位-1023~1024 |
决定浮点数的精度 float 尾数部分23位,换算成十进制为223 =8388608,因此精度为6~7位 double 尾数部分23位,换算成十进制为252 =4503599627370496,因此精度为15~16位 |
结论
浮点数交给计算机存储的,可能会有精度的丢失问题,出了问题的话,在大型的项目中,是很难找出问题的,因此提前做好规划与计算是有必要的。

计算实例
第一个例子
把十进制小数0.475转换成二进制,具体应该怎么操作?
1. 将小数划分成整数+小数两部分
2. 整数部分转换
转换采用除2取余法,此处的0.475的整数部分为0,不需要操作。
3. 小数部分转换
转换采用乘2取整法。详细看下图

3. 合并结果
整数部分+小数部分,得到二进制结果为 0.101.
根据IEEE754标准,即符号位+尾数+阶码的计数方式,可以表示为
1.01 × 2-1
- 符号位:0
- 阶码部分:以float为例子,则为 127 + (-1)=126,所以二进制为:01111110
- 尾数部分:以float为例子,应为 23位,尾数补齐之后为0100000000000000000000
最终结果为(以float表示)
0011111100100000000000000000000
第二个例子
把十进制小数8.26转换成二进制,具体应该怎么操作?

整数部分+小数部分 得到二进制结果为1000.0100001 .....
根据IEEE754标准,即符号位+尾数+阶码的计数方式,可以表示为
1.0000100001 × 2 3
- 符号位:0
- 阶码部分:以float为例子,则为 127 + (3)=130,所以二进制为:10000010
- 尾数部分:
0.0000100001...,,它本身无限不循环,但是如果以 float 为例子,截取 23位,表示为00001000010100011110110
最终结果为(以float表示)
01000001 00000100 00101000 11110110
因此,对于这种无限位数的小数,用计算机去存储必然会导致精度的损失。所以,各位在使用过程中一定要谨慎小心。
结语
浮点数转换为二进制就讲解到这里了,觉得有用的老铁们,请点赞关注我吧,另外,关注我的老铁们可以私聊我,获取浮点数转换为二进制的神器,这样子,再也不用自己手撕浮点数转为二进制了。
