图的深度优先遍历和广度优先遍历

深度优先遍历是纵向遍历，一直到底，二叉树的前序遍历、中序遍历，后序遍历都是深度优先遍历。　　

广度优先遍历是横向遍历，层次遍历，遍历完一层再遍历下一层，直到遍历所有元素。

以矩阵为例，分析深度优先遍历（DFS）和广度优先遍历的路径：

插入矩阵：

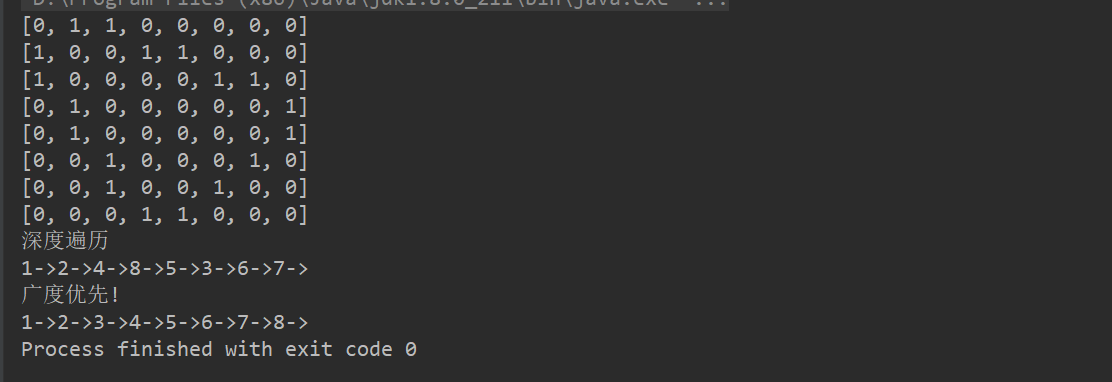
　　　　//测试一把图是否创建ok
        int n = 8;  //结点的个数
        String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};
        //创建图对象
        Graph graph = new Graph(n);
        //循环的添加顶点
        for (String vertex : Vertexs) {
            graph.insertVertex(vertex);
        }
        //更新边的关系
        graph.insertEdge(0, 1, 1);
        graph.insertEdge(0, 2, 1);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(1, 4, 1);
        graph.insertEdge(3, 7, 1);
        graph.insertEdge(4, 7, 1);
        graph.insertEdge(2, 5, 1);
        graph.insertEdge(2, 6, 1);
        graph.insertEdge(5, 6, 1);

矩阵：

　　

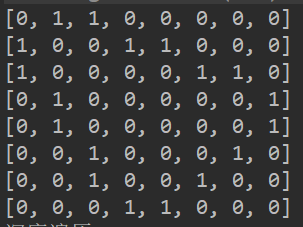
深度优先遍历路径：1->2->4->8->5->3->6->7->

　　

广度优先遍历路径：1->2->3->4->5->6->7->8->

　　

代码实现：

package wy.datastructures.graph;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;

public class Graph {

    private int[][] edges;
    private List<String> vertexList;
    private int numOfEdges;
    private boolean[] isVisited;

    public static void main(String[] args) {
        //测试一把图是否创建ok
        int n = 8;  //结点的个数
        String Vertexs[] = {"1", "2", "3", "4", "5", "6", "7", "8"};

        //创建图对象
        Graph graph = new Graph(n);
        //循环的添加顶点
        for (String vertex : Vertexs) {
            graph.insertVertex(vertex);
        }

        //更新边的关系
        graph.insertEdge(0, 1, 1);
        graph.insertEdge(0, 2, 1);
        graph.insertEdge(1, 3, 1);
        graph.insertEdge(1, 4, 1);
        graph.insertEdge(3, 7, 1);
        graph.insertEdge(4, 7, 1);
        graph.insertEdge(2, 5, 1);
        graph.insertEdge(2, 6, 1);
        graph.insertEdge(5, 6, 1);


        //显示一把邻结矩阵
        graph.showGraph();

        //测试一把，我们的dfs遍历是否ok
        System.out.println("深度遍历");
        graph.dfs(); // A->B->C->D->E [1->2->4->8->5->3->6->7]
        System.out.println();
        System.out.println("广度优先!");
        graph.bfs(); // A->B->C->D-E [1->2->3->4->5->6->7->8]
    }

    public void dfs(int index) {
        isVisited[index] = true;
        System.out.print(getVertex(index) + "->");
        for (int i = 0; i < getNumOfVertex(); i++) {
            if (edges[index][i] == 1 && !isVisited[i]) {
                dfs(i);
            }
        }
    }

    public void dfs() {
        isVisited = new boolean[vertexList.size()];
        dfs(0);
    }

    public void bfs() {
        isVisited = new boolean[vertexList.size()];
        LinkedList<Integer> queue = new LinkedList<>();
        for (int x = 0; x < getNumOfVertex(); x++) {
            if (!isVisited[x]) {
                isVisited[x] = true;
                System.out.print(getVertex(x) + "->");
                queue.addLast(x);
                while (!queue.isEmpty()) {
                    int index = queue.removeFirst();
                    for (int y = 0; y < getNumOfVertex(); y++) {
                        if (edges[index][y] == 1 && !isVisited[y]) {
                            isVisited[y] = true;
                            queue.addLast(y);
                            System.out.print(getVertex(y) + "->");
                        }
                    }
                }
            }
        }
    }

    public Graph(int n) {
        edges = new int[n][n];
        vertexList = new ArrayList<>(n);
        numOfEdges = 0;
        isVisited = new boolean[n];
    }

    public int getNumOfEdges() {
        return numOfEdges;
    }

    public int getNumOfVertex() {
        return vertexList.size();
    }

    public String getVertex(int index) {
        return vertexList.get(index);
    }

    public int getIndexOfVertex(String vertex) {
        return vertexList.indexOf(vertex);
    }

    public int getEdge(int v1, int v2) {
        return edges[v1][v2];
    }

    public void insertVertex(String vertex) {
        vertexList.add(vertex);
    }

    public void insertEdge(int v1, int v2, int weight) {
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;
        numOfEdges++;
    }

    public void showGraph() {
        for (int[] link : edges) {
            System.out.println(Arrays.toString(link));
        }
    }

}

输出结果：