剑指offer题目--解决面试题的思路

19 二叉树的镜像

递归实现

public class Solution {
    public void Mirror(TreeNode root) {
        if(root == null || 
           (root.left == null && root.right == null)){
            return;
        }
        TreeNode temp = root.left;
        root.left = root.right;
        root.right = temp;
        if(root.left != null){
            Mirror(root.left);
        }
        if(root.right != null){
            Mirror(root.right);
        }
    }
}

循环实现

import java.util.Stack;
public class Solution {
    public void Mirror(TreeNode root) {
        if(root == null){
            return;
        }
        Stack<TreeNode> stack = new Stack<TreeNode>();
        stack.push(root);
        while(!stack.isEmpty()){
            TreeNode node = stack.pop();
            if(node.left != null||node.right != null){
                TreeNode temp = node.left;
                node.left = node.right;
                node.right = temp;
            }
            if(node.left!=null){
                stack.push(node.left);
            }
            if(node.right!=null){
                stack.push(node.right);
            }
        }
    }
}

20 顺时针打印矩阵

import java.util.ArrayList;
public class Solution {
    public ArrayList<Integer> printMatrix(int [][] matrix) {
        ArrayList<Integer> result = new ArrayList<Integer> ();
        if(matrix.length==0) return result;
        int row = matrix.length,col = matrix[0].length;
        if(col==0) return result;
        
         // 定义四个关键变量，表示左上和右下的打印范围
        int left = 0, top = 0, right = col - 1, bottom = row - 1;
        while(left <= right && top <= bottom){
            // left to right
            for (int i = left; i <= right; ++i)  result.add(matrix[top][i]);
            // top to bottom
            for (int i = top + 1; i <= bottom; ++i)  result.add(matrix[i][right]);
            // right to left
            if (top != bottom)
            for (int i = right - 1; i >= left; --i)  result.add(matrix[bottom][i]);
            // bottom to top
            if (left != right)
            for (int i = bottom - 1; i > top; --i)  result.add(matrix[i][left]);
            left++;top++;right--;bottom--;
        }
        return result;    
    }
}

class Solution {
public:
    vector<int> printMatrix(vector<vector<int> > matrix) {
        int row = matrix.size();
        int col = matrix[0].size();
        vector<int> res;
         
        // 输入的二维数组非法，返回空的数组
        if (row == 0 || col == 0)  return res;
         
        // 定义四个关键变量，表示左上和右下的打印范围
        int left = 0, top = 0, right = col - 1, bottom = row - 1;
        while (left <= right && top <= bottom)
        {
            // left to right
            for (int i = left; i <= right; ++i)  res.push_back(matrix[top][i]);
            // top to bottom
            for (int i = top + 1; i <= bottom; ++i)  res.push_back(matrix[i][right]);
            // right to left
            if (top != bottom)
            for (int i = right - 1; i >= left; --i)  res.push_back(matrix[bottom][i]);
            // bottom to top
            if (left != right)
            for (int i = bottom - 1; i > top; --i)  res.push_back(matrix[i][left]);
            left++,top++,right--,bottom--;
        }
        return res;
    }
};

21 包含min函数的栈

Stack实现

import java.util.Stack;
public class Solution {
    Stack<Integer> stack1 = new Stack<Integer>();
    Stack<Integer> stack2 = new Stack<Integer>();
    public void push(int node) {
        stack1.push(node);
        if(stack2.isEmpty() || node < stack2.peek()){
            stack2.push(node);
        }else{
            stack2.push(stack2.peek());
        }
    }
    
    public void pop() {
        assert(!stack1.isEmpty() && !stack2.isEmpty());
        stack1.pop();
        stack2.pop();
    }
    
    public int top() {
        return stack1.peek();
    }
    
    public int min() {
        return stack2.peek();
    }
}

ArrayList实现

import java.util.ArrayList;
 
public class Solution {
 
    ArrayList<Integer> list = new ArrayList<Integer>();
     
    public void push(int node) {
        list.add(0,node);
    }
     
    public void pop() {
        list.get(0);
        list.remove(0);
    }
     
    public int top() {
        return list.get(0).intValue();
    }
 
    public int min() {
        int temp = top();
        for(int i=1;i<list.size();i++){
            if(temp>list.get(i).intValue()){
                temp = list.get(i).intValue();
            }
        }
        return temp;
    }
}

22 栈的压入、弹出序列

 Stack实现

import java.util.ArrayList;
import java.util.Stack;

public class Solution {
    public boolean IsPopOrder(int [] pushA,int [] popA) {
      boolean bResult = false;
      int nLength = pushA.length;
      if(pushA != null && popA != null &&  nLength>0){
          int nextpush =0;
          int nextpop = 0;
          Stack<Integer> stackData = new Stack<Integer>();
          while(nextpop < nLength){
              while(stackData.empty() || stackData.peek() != popA[nextpop]){
                  if(nextpush == nLength){
                      break;
                  }
                  stackData.push(pushA[nextpush]);
                  nextpush++;
              }
              if(stackData.peek() != popA[nextpop]){
                  break;
              }
              stackData.pop();
              nextpop++;
          }
          if(stackData.empty() && nextpop == nLength){
              bResult = true;
          }
      }
        return bResult;
    }
}

23 从上往下打印二叉树

按层打印，实际就是广度优先搜索 BFS, 借助一个队列就可以实现.

广度优先搜索 BFS：主要借助一个队列、一个布尔类型数组、邻接矩阵完成（判断一个点是否查看过，用于避免重复到达同一个点，造成死循环等），先将各点以及各点的关系存入邻接矩阵。

再从第一个点开始，将一个点存入队列，然后在邻接表中找到他的相邻点，存入队列，每次pop出队列头部并将其打印出来（文字有些抽象，实际过程很简单），整个过程有点像往水中投入石子水花散开。

public class Solution {
    public ArrayList<Integer> PrintFromTopToBottom(TreeNode root) {
        ArrayList<Integer> list = new ArrayList<>();
        ArrayList<TreeNode> queue = new ArrayList<>();
        if (root == null) {
            return list;
        }
        queue.add(root);
        while (queue.size() != 0) {
            TreeNode temp = queue.remove(0);
            if (temp.left != null){
                queue.add(temp.left);
            }
            if (temp.right != null) {
                queue.add(temp.right);
            }
            list.add(temp.val);
        }
        return list;
    }
}

扩展：

广度优先遍历一个有向图，同样可以基于队列实现。树是图的一种特殊退化形式，从上到下按层遍历二叉树，本质上就是广度优先遍历二叉树。

24 二叉搜索树的后序遍历序列

后序遍历：先遍历子结点，再遍历父结点。在后序遍历得到的序列中，最后一个数字是树的根结点。

public class Solution {
    public boolean VerifySquenceOfBST(int [] sequence) {
        if(sequence == null || sequence.length <= 0){
            return false;
        }
        int root = sequence[sequence.length-1];
        
        int[] sequenceleft = new int[sequence.length];
        int[] sequenceright = new int[sequence.length];
        
        //在二叉搜索树中左子树的结点小于结点
        int i=0;
        for(;i<sequence.length -1;++i){
            if(sequence[i] > root){
                break;
            }
            sequenceleft[i] = sequence[i];
        }
        
        //早二叉搜索树中右子树的结点大于根结点
        int j=i;
        int k=0;
        for(;j < sequence.length -1;++j){
            if(sequence[j] < root){
                return false;
            }
            k++;
            sequenceright[k] = sequence[j];
        }
        
        //判断左子树是不是二叉搜索树
        boolean left = true;
        if(i>0){
            left = VerifySquenceOfBST(sequenceleft);
        }
        
        boolean right = true;
        if(i<sequence.length-1){
            right = VerifySquenceOfBST(sequenceright);
        }
        return (left && right);        
    }
}

 前中后序遍历

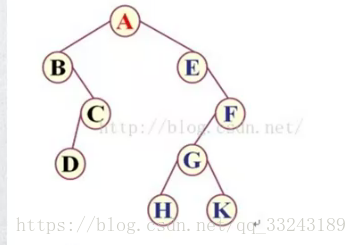
前、中、后指的是根节点的顺序。前序遍历有根节点开始。

前序遍历：ABCDEFGHK

中序遍历：BDCAEHGKF

后序遍历：DCBHKGFEA

中序排列思想：

25 二叉树中和为某一值的路径

public class Solution {
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
        ArrayList<ArrayList<Integer>> paths=new ArrayList<ArrayList<Integer>>();
        if(root==null)return paths;
        find(paths,new ArrayList<Integer>(),root,target);
        return paths;
    }
    
    public void find(ArrayList<ArrayList<Integer>> paths,ArrayList<Integer> path,TreeNode root,int target){
            path.add(root.val);
            if(root.left==null&&root.right==null){
                if(target==root.val){
                    paths.add(path);
                }
                return;
            }
            ArrayList<Integer> path2=new ArrayList<>();
            path2.addAll(path);
            if(root.left!=null)find(paths,path,root.left,target-root.val);
            if(root.right!=null)find(paths,path2,root.right,target-root.val);
        }
}

import java.util.ArrayList;
import java.util.Stack;
/**
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
    public ArrayList<ArrayList<Integer>> FindPath(TreeNode root,int target) {
        ArrayList<ArrayList<Integer>> pathList=
                new ArrayList<ArrayList<Integer>>();
        if(root==null)
            return pathList;
        Stack<Integer> stack=new Stack<Integer>();
        FindPath(root,target,stack,pathList );
        return pathList;
    }
    
    private void FindPath(TreeNode root, int target,
            Stack<Integer> path,
            ArrayList<ArrayList<Integer>> pathList) {
        if(root==null)
            return;
        if(root.left==null&&root.right==null){
            if(root.val==target){
                ArrayList<Integer> list=
                        new ArrayList<Integer>();
                for(int i:path){
                    list.add(new Integer(i));
                }
                list.add(new Integer(root.val));
                pathList.add(list);
            }
        }
        else{
            path.push(new Integer(root.val));
            FindPath(root.left, target-root.val, path, pathList);
            FindPath(root.right, target-root.val, path,  pathList);
            path.pop();
        }
    }
}

26 复杂链表的复制

分治法，通常分治法的思路都可以用递归实现

在复杂链表的结点中，除了有指向下一个结点的指针，还有指向任意结点的指针。、

/*
public class RandomListNode {
    int label;
    RandomListNode next = null;
    RandomListNode random = null;

    RandomListNode(int label) {
        this.label = label;
    }
}
*/
public class Solution {
    public RandomListNode Clone(RandomListNode pHead)
    {
        CloneNodes(pHead);
        ConnectSiblingNodes(pHead);
        return ReconnectNodes(pHead);
    }
    
    void CloneNodes(RandomListNode pHead){
        RandomListNode pNode = pHead;
        while(pNode != null){
            RandomListNode pCloned = new RandomListNode(pNode.label);
            pCloned.next = pNode.next;
            pCloned.random = null;
            
            pNode.next = pCloned;
            pNode = pCloned.next;
        }
    }
    
    void ConnectSiblingNodes(RandomListNode pHead){
        RandomListNode pNode = pHead;
        while(pNode!= null){
            RandomListNode pCloned = pNode.next;
            if(pNode.random != null){
                pCloned.random = pNode.random.next;
            }
            pNode = pCloned.next;
            
        }
    }
    
    RandomListNode ReconnectNodes(RandomListNode pHead){
        RandomListNode pNode = pHead;
        RandomListNode pClonedHead = null;
        RandomListNode pClonedNode = null;
        
        if(pNode != null){
            pClonedNode = pNode.next;
            pClonedHead = pClonedNode;
            pNode.next = pClonedNode.next;
            pNode = pNode.next;
        }
        
        while(pNode != null){
            pClonedNode.next = pNode.next;
            pClonedNode = pClonedNode.next;
            pNode.next = pClonedNode.next;
            pNode = pNode.next;
        }
        return pClonedHead;
    }
}

27 二叉搜索树与双向链表

二叉搜索树：左子结点的值小于父结点的值，右子节点的值大于父结点的值。

直接递归

public class Solution {
    public TreeNode Convert(TreeNode pRootOfTree) {
        if(pRootOfTree == null) return pRootOfTree;
        pRootOfTree = ConvertNode(pRootOfTree);
        while(pRootOfTree.left!= null) pRootOfTree = pRootOfTree.left;
        return pRootOfTree;
    }
    
    TreeNode ConvertNode(TreeNode root)
    {
        if(root == null) return root;
        if(root.left != null)
        {
            TreeNode left = ConvertNode(root.left);
            while(left.right!= null) left = left.right;
            left.right = root;
            root.left = left;
        }
         
        if(root.right != null)
        {
            TreeNode right = ConvertNode(root.right);
            while(right.left!= null) right = right.left;
            right.left = root;
            root.right = right;
        }
        return root;
    }
}

此解法暂时未通过

public class Solution {
    public TreeNode Convert(TreeNode pRootOfTree) {
        TreeNode pLastNodeInList = null;
        ConvertNode(pRootOfTree, pLastNodeInList);
        
        //pLastNodeInList双向链表尾结点
        //需要返回头结点
        TreeNode pHeadOfList = pLastNodeInList;
            while(pHeadOfList != null && pHeadOfList.left != null){
                pHeadOfList = pHeadOfList.left;
            }
        return pHeadOfList;
    }
    
    void ConvertNode(TreeNode pNode, TreeNode pLastNodeInList){
        if(pNode == null){
            return;
        }
        TreeNode pCurrent = pNode;
        if(pCurrent.left != null){
           ConvertNode(pCurrent.left, pLastNodeInList);
        }
        
        pCurrent.left = pLastNodeInList;
        if(pLastNodeInList != null){
            pLastNodeInList.right = pCurrent;
        }
        
        pLastNodeInList = pCurrent;
        
        if(pCurrent.right != null){
            ConvertNode(pCurrent.right,pLastNodeInList);
        }
    }
}

28 字符串的排列

 解法一：递归

import java.util.ArrayList;
import java.util.Collections;
import java.util.Set;
import java.util.HashSet;
public class Solution {
    public ArrayList<String> Permutation(String str) {
        ArrayList<String> list = new ArrayList<String>();
        if(str!=null && str.length()>0){
            PermutationHelper(str.toCharArray(),0,list);
            Collections.sort(list);
        }
        return list;
    }

    private void PermutationHelper(char[] chars,int i,ArrayList<String> list){
        if(i == chars.length-1){
            list.add(String.valueOf(chars));
        }else{
            Set<Character> charSet = new HashSet<Character>();
            for(int j=i;j<chars.length;++j){
                if(j==i || !charSet.contains(chars[j])){
                    charSet.add(chars[j]);
                    swap(chars,i,j);
                    PermutationHelper(chars,i+1,list);
                    swap(chars,j,i);
                }
            }
        }
    }
 
    private void swap(char[] cs,int i,int j){
        char temp = cs[i];
        cs[i] = cs[j];
        cs[j] = temp;
    }
}

解法二：字典序排列算法

import java.util.ArrayList;
import java.util.Arrays;
public class Solution {
    public ArrayList<String> Permutation(String str) {
        ArrayList<String> list = new ArrayList<String>();
        if(str==null || str.length()==0){
            return list;
        }
        char[] chars = str.toCharArray();
        Arrays.sort(chars);
        list.add(String.valueOf(chars));
        int len = chars.length;
        while(true){
            int lIndex = len-1;
            int rIndex;
            while(lIndex>=1 && chars[lIndex-1]>=chars[lIndex]){
                lIndex--;
            }
            if(lIndex == 0)
                break;
            rIndex = lIndex;
            while(rIndex<len && chars[rIndex]>chars[lIndex-1]){
                rIndex++;
            }
            swap(chars,lIndex-1,rIndex-1);
            reverse(chars,lIndex);
 
            list.add(String.valueOf(chars));
        }
 
        return list;
    }
    
    private void reverse(char[] chars,int k){
        if(chars==null || chars.length<=k)
            return;
        int len = chars.length;
        for(int i=0;i<(len-k)/2;i++){
            int m = k+i;
            int n = len-1-i;
            if(m<=n){
                swap(chars,m,n);
            }
        }
 
    }
 
    private void swap(char[] cs,int i,int j){
        char temp = cs[i];
        cs[i] = cs[j];
        cs[j] = temp;
    }
}

参考：

https://www.cnblogs.com/cxjchen/p/3932949.html

https://www.cnblogs.com/pmars/archive/2013/12/04/3458289.html