[LeetCode]96. 不同的二叉搜索树(DP，卡特兰数)

题目

给定一个整数 n，求以 1 ... n 为节点组成的二叉搜索树有多少种？

示例:

输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
           /     /      /       
     3     2     1      1   3      2
    /     /                        
   2     1         2                 3

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/unique-binary-search-trees
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题解

• 指定节点个数的BST的种类是固定的，可以容易想到递归：左子树*右子树 且每个节点轮流做根结点 即得到所有可能。使用DP来做。
• 以三个节点为例，用dp[3]表示
  dp[3]=dp[0]dp[2]+dp[1]dp[1]+dp[2]*dp[0]
• 故转移方程：
  dp[n]+=dp[i]*dp[n-i-1] (i=0,1,...n-1)

其他

• 卡特兰数是组合数学中一个常出现在各种计数问题中出现的数列。
  
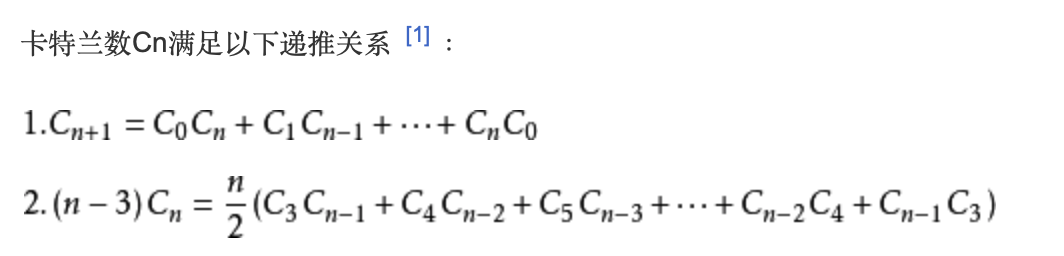
• 本题的dp数组即是卡特兰数

代码

class Solution {
 	public int numTrees(int n) {
		if (n <= 0) {
			return 0;
		}
		if (n == 1) {
			return 1;
		}

		int[] dp = new int[n + 1];
		dp[0] = 1;
		dp[1] = 1;
		for (int nodeCnt = 2; nodeCnt <= n; ++nodeCnt) {// nodeCnt个节点的BST
			for (int j = 0; j < nodeCnt; ++j) { // 根的左子树有j个节点
				dp[nodeCnt] += dp[j] * dp[nodeCnt - j - 1];
			}
		}

		return dp[n];
	}
}