Commonly Used Data Structures And Time Complexity

Trie

Time Complexity

Insert/search O(l), l is the length of the word

Space Complexity

O(prefixes), O(n * l * l) n words with length l

Binary Search Tree

H is the height of the tree, if the tree is balanced, h = logn

Data Structure	get	search	insert	delete
Array	O(1)	O(n)	O(n)	O(n)
ArrayList	O(1)	O(n)	O(1)	O(1)
LinkedList	O(n)	O(n)	O(1)	O(1)
Stack	O(n)	O(n)	O(1)	O(1)
PriorityQueue	O(logn)	O(n)	O(logn )	O(n)
HashMap	O(1)	O(1)	O(1)	O(1)
TreeMap	O(logn)	O(n)	O(logn)	O(logn)
HashSet	O(1)	O(1)	O(1)	O(1)
Trie	O(L)	O(L)	O(L)	O(L)
B Tree	O(logn)	O(logn)	O(logn)	O(logn)
Binary Search Tree	O(h)	O(h)	O(h)	O(h)

 

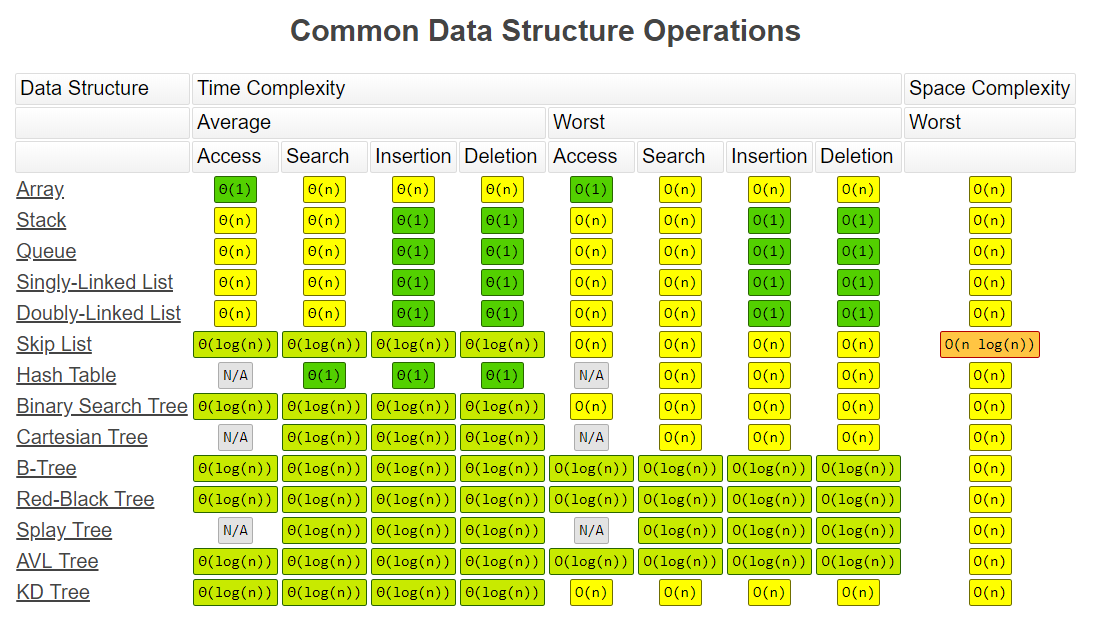
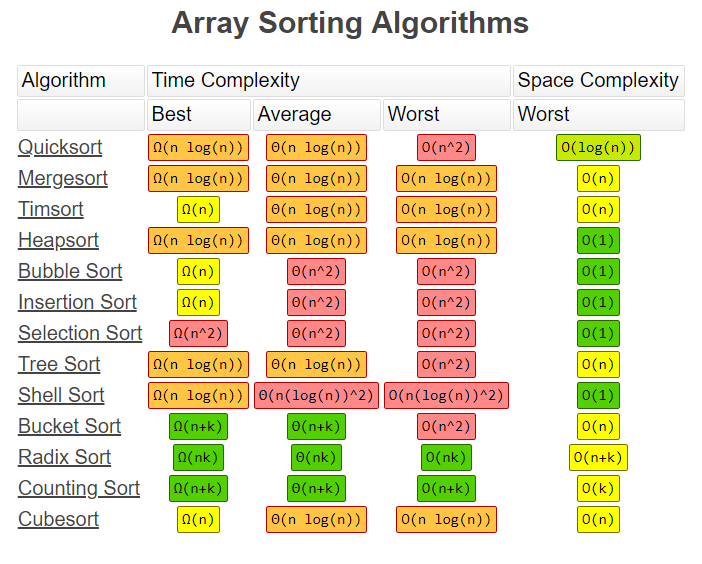
Master Theorem Cheatsheet

Equation	Time	Space	Examples
T(n) = 2*T(n/2) + O(n)	O(nlogn)	O(logn)	quick_sort
T(n) = 2*T(n/2) + O(n)	O(nlogn)	O(n + logn)	merge_sort
T(n) = T(n/2) + O(1)	O(logn)	O(logn)	Binary search
T(n) = 2*T(n/2) + O(1)	O(n)	O(logn)	Binary tree traversal
T(n) = T(n-1) + O(1)	O(n)	O(n)	Binary tree traversal
T(n) = T(n-1) + O(n)	O(n^2)	O(n)	quick_sort(worst case)
T(n) = n * T(n-1)	O(n!)	O(n)	permutation
T(n) = T(n-1)+T(n-2)+…+T(1)	O(2^n)	O(n)	combination

    @Test
    public void testQueue() {
        Queue<String> queue = new LinkedList<>();
        queue.offer("a");
        queue.offer("b");
        System.out.println(queue.peek()); // a
        System.out.println(queue.poll()); // a
    }

    @Test
    public void testStack() {
        Stack<String> stack = new Stack<>();
        stack.push("a");
        stack.push("b");
        System.out.println(stack.peek()); // b
        System.out.println(stack.pop());  // b
    }

    @Test
    public void testDeque() {
        Deque<String> deque = new LinkedList<>();
        String[] array = {"1", "2", "3", "4"};

        // used as a stack
        for (String ele: array) {
            deque.push(ele);
        }
        System.out.println(deque.peekFirst()); // 4
        System.out.println(deque.peekLast());  // 1
        System.out.println(deque.pop());  // 4
        System.out.println(deque.removeFirst());  // 3
        System.out.println(deque.removeLast());  // 1

        deque.clear();

        // used as a queue
        for (String ele: array) {
            deque.offer(ele);
        }
        System.out.println(deque.peekFirst()); // 1
        System.out.println(deque.peekLast());  // 4
        System.out.println(deque.poll());  // 1
        System.out.println(deque.removeFirst());  // 2
        System.out.println(deque.removeLast());  // 4
    }

    @Test
    public void testPriorityQueue() {
        Integer[] array = {3, 1, 4, 2};
        // By default it is a min heap
        PriorityQueue<Integer> minHeap = new PriorityQueue<>();
        for (Integer ele: array) {
            minHeap.offer(ele);
        }

        System.out.println(minHeap.poll());  // 1

        // Create a max heap
        PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());
        // PriorityQueue<Integer> maxHeap = new PriorityQueue<>((x, y) -> y - x);

        for (Integer ele: array) {
            maxHeap.offer(ele);
        }

        System.out.println(maxHeap.poll());  // 4
    }