递归改动态规划

递归是一种尝试，比如我不知道一个问题的解决方法，但是我知道怎么去尝试。

左神说图灵就是将计算机用于尝试，在此之前，都是知道解决问题的固定方法，然后用计算机来解决。因此被誉为计算机之父。

其实最早使用计算机的是拜伦的女儿。第一位计算机程序员是女性哦。

 

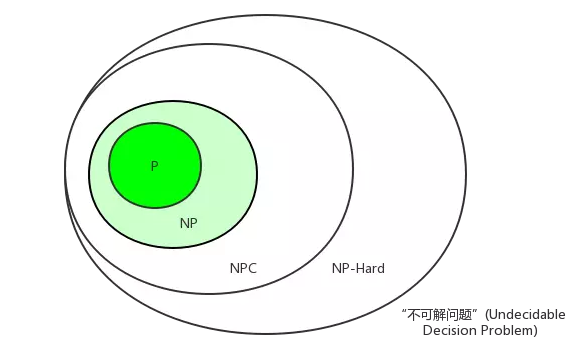
P问题：是否可以在多项式时间内求出问题的解

NP问题：可以在多项式的时间里验证（猜出）一个解的问题。

NPC(NP-完全问题)：1、是一个NP问题 　　2、所有的NP问题都可以约化到它

约化(Reducibility，归约)：一个问题A可以约化为问题B的含义即是，可以用问题B的解法解决问题A，或者说，问题A可以“变成”问题B。“问题A可约化为问题B”有一个重要的直观意义：B的时间复杂度高于或者等于A的时间复杂度。而且，约化具有传递性。

 NP-Hard问题：满足NPC问题定义的第二条但不一定要满足第一条，所有的NP问题都可以约化到它，但是他不一定是NP问题。

题目1：给定二维数组，从左上角到右下角，每一步只能向下或者向右，沿途经过的数累加，返回最小路径和

package day6;
/*
 *     给定二维数组，从左上角到右下角，每一步只能向下或者向右，
 *     沿途经过的数累加，返回最小路径和
 * 
 *     从(0,0)------>(n,n)
 */
public class Code06_PathMinSum {
    //递归(会重复计算)
    public static int getMin1(int arr[][],int i, int j, int sum) {
        if (i== arr.length -1 && j == arr[0].length -1) {
            sum= arr[i][j];
        }
        else if (i == arr.length -1) {
            sum=  arr[i][j]+getMin1(arr,i,j+1,sum);
        }
        else if (j == arr[0].length -1) {
            sum=  arr[i][j]+getMin1(arr,i+1,j,sum);
        }
        else {    
            sum=  arr[i][j] +Math.min(getMin1(arr,i+1,j,sum), getMin1(arr,i,j+1,sum));
        }
        return sum;
    }
    //动态规划
    public static int getMin2(int arr[][]) {
        //考虑不存在的情况啊
        if(arr == null || arr.length ==0 || arr[0] == null || arr[0].length == 0) {
            return 0;
        }
        int n = arr.length -1;
        int m = arr[0].length -1;
        int  srr[][] = new int [n+1][m+1];
        for (int i = n ;i >=0 ;i--){
            for(int j = m ;j>=0 ;j--){
                if (i == n && j == m) {
                    srr[n][m] = arr[n][m];
                }
                else if(i == n) {
                    srr[i][j]=arr[i][j] + srr[i][j+1];
                }
                else if (j == m) {
                    srr[i][j]= arr[i][j] + srr[i+1][j];
                    
                }else {
                    srr[i][j] =arr[i][j]+ Math.min(srr[i+1][j],srr[i][j+1] );
                    
                }
            }    
        }
        return srr[0][0];
    }
    
    
    
    // for test
    public static int[][] generateRandomMatrix(int rowSize, int colSize) {
        if (rowSize < 0 || colSize < 0) {
            return null;
        }
        int[][] result = new int[rowSize][colSize];
        for (int i = 0; i != result.length; i++) {
            for (int j = 0; j != result[0].length; j++) {
                result[i][j] = (int) (Math.random() * 10);
            }
        }
        return result;
    }
    
    
    //test
    public static void main(String[] args) {
        int arr[][] = {
                {3,2,1,0,},
                {7,5,0,1,},
                {3,7,6,2,},
        };
        
        System.out.println(getMin1(arr,0,0,0));
        System.out.println(getMin2(arr));
        
        
        arr = generateRandomMatrix(6, 7);
        System.out.println(getMin1(arr,0,0,0));
        System.out.println(getMin2(arr));
        
        
    }

}

题目2：给定一个数组arr[]，和一个数aim，从数组中任意选数，问是否可以能累加得到aim，能返回true，不能返回false

package day6;
/*
 *     给定一个数组arr，和一个数aim
 *     从数组中任意选数，问是否可以能累加得到aim，
 *     能返回true，不能返回false
 */
public class Code07_CanGetAim {
    
    public static boolean canGetAim(int arr[],int aim) {
        return  fun1(arr, 0,aim,0);
        
    }    
    //递归
    public static boolean fun1(int arr[] , int n ,int aim,int sum) {
        if (sum == aim) {
            return true;
        }
        if(n == arr.length) {
            return false;
        }
        return fun1(arr ,n+1,aim,sum+arr[n]) || fun1(arr ,n+1,aim,sum) ;
    }
    
    
    //动态规划
    
    public static boolean fun2(int arr[],int aim) {
        if (arr == null) return false;
        //预处理，数组中可能有正数，也可能有负数
        //sum 的范围 minn ~ maxx  共 maxx -minn +1个数 
        //对应下标（偏移） 坐标+min
        int maxx = 0, minn = 0;
        for (int i = 0 ; i < arr.length ;i ++) {
            if (arr[i] >0) {
                maxx += arr[i];
            }else {
                minn+= arr[i];
            }
        }
        if (aim >maxx || aim < minn) return false;    //保证aim在区间里
        
        int num =arr.length;
        int sum = maxx-minn;
        boolean dp[][] = new boolean [num+1][sum+1];
        //System.out.println(minn +" " +maxx);
        
        //一个是赋值一列，一个是赋值一个 ,效果一样
        //aim 是数，数变下标是 -min
        
        //dp[num][aim-minn] = true;
        for (int i = num; i>0;i--) {
            dp[i][aim-minn] = true;
        }
        

        
        for (int i = num-1 ; i>=0 ;i--) {
            for (int j =0; j<sum ;j++) {
                //j是下标，j表示的数 j+minn,下标变数+min            
                if (j+arr[i] > sum || j+arr[i] < 0) {
                    dp[i][j]= dp[i+1][j]; 
                }else {
                    dp[i][j]= (dp[i+1][j] || dp[i+1][j+arr[i]]);
                }
                    
            }
        }
        
        return dp[0][0];
        
    }
    
    // for test
    public static int[] generateRandomMatrix(int maxSize, int maxValue) {
        if (maxSize < 0 ) {
            return null;
        }
        int[] result = new int[maxSize];
        for (int i = 0; i != result.length; i++) {
                result[i] = (int) (Math.random() * maxValue);
        }
        return result;
    }

    public static void  printArrays(int arr[]) {
        for (int i = 0 ; i< arr.length ; i++) {
            System.out.print(arr[i]+" ");
        }
        System.out.println();
    }
    
    public static void main(String[] args) {
//        int arr[]= {3,2,7,13};//{3,2,1,-1};
//        int aim = 4;//9;
//        System.out.println(canGetAim(arr, aim));
//        System.out.println(fun2(arr, aim));
        int n =100,maxSize = 20,maxValue = 8,aim =44;
        boolean flag = true;
        for (int i = 0 ; i <n ; i ++) {
            int arr[] = generateRandomMatrix(maxSize, maxValue);
            if(fun2(arr, aim) != canGetAim(arr, aim)) {
                flag = false;
                printArrays(arr);
                System.out.println(canGetAim(arr, aim));
                System.out.println(fun2(arr, aim));
                break;
            }
        }
        System.out.println(flag ? "Nice!":"WOw!!!!Problem show up !!!!!!!"); 
        
    }
}

可以将动态规划中return dp[0][0]前的for循环替换成下面，效果相同，更简洁。核心代码就这一点。可对比递归。

        //这样写更加简洁，道理相同
        for (int i = num-1 ; i>=0 ;i--) {
            for (int j =sum; j>=0 ;j--) {//注意这里的j必须从后往前
                //j是下标，j表示的数 j+minn,下标变数+min                
                dp[i][j]= dp[i+1][j]; 
                if (j+arr[i] <=sum &&  j+arr[i] >= 0) {
                    dp[i][j]= (dp[i][j] || dp[i+1][j+arr[i]]);
                }                
            }
        }

 总结——递归改动态规划：

一、条件

　　1，有重复的状态

　　2，无后效应问题。即状态与路径无关（到达这个状态之后，无论怎么到达这个状态的，往后走的路与前面无关。类似于入此门，前尘往事尽斩断），进一步讲，可变参数确定之后，返回值就确定了。

二、方法（套路）

　　1，按照要求写出递归版本

　　2，找到需要求解的位置

　　3，回到basecase中，将不被依赖的位置设置好（如题2就是最后一行）

　　4，回到一般位置（情况），找到依赖关系。