[LeetCode] Linked List Cycle II, Solution

Given a linked list, return the node where the cycle begins. If there is no cycle, return null.

Follow up:
Can you solve it without using extra space?

[Thoughts]

首先，比较直观的是，先使用Linked List Cycle I的办法，判断是否有cycle。如果有，则从头遍历节点，对于每一个节点，查询是否在环里面，是个O(n^2)的法子。但是仔细想一想，发现这是个数学题。

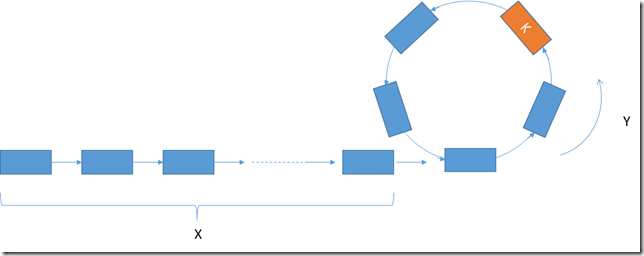
如下图，假设linked list有环，环长Y，环以外的长度是X。

现在有两个指针，第一个指针，每走一次走一步，第二个指针每走一次走两步，如果他们走了t次之后相遇在K点

那么       指针一  走的路是      t = X + nY + K        ①

             指针二  走的路是     2t = X + mY+ K       ②          m,n为未知数

把等式一代入到等式二中, 有

2X + 2nY + 2K = X + mY + K

=>   X+K  =  (m-2n)Y    ③

这就清晰了，X和K的关系是基于Y互补的。等于说，两个指针相遇以后，再往下走X步就回到Cycle的起点了。这就可以有O(n)的实现了。

[Code]

 1     ListNode *detectCycle(ListNode *head) {
 2         ListNode * first = head;
 3         ListNode * second = head;
 4         
 5         while(first != NULL && second != NULL)
 6         {
 7             first = first->next;
 8             second = second->next;
 9             if(second != NULL)
10                 second = second->next;
11             if(first == second)
12                 break;
13         }
14         
15         if(second == NULL) return NULL;
16         
17         // 一起往下走X步，就找到节点了。
18         first = head;
19         while(first!=second)
20         {
21             first = first->next;
22             second = second->next;
23         }
24         
25         return second;
26     }