You are giving candies to these children subjected to the following requirements:
- Each child must have at least one candy.
- Children with a higher rating get more candies than their neighbors.
[Thoughts]
蛮好玩的题。感觉用dp简单点。定义Candy[i]为第i个孩子需要给的最少的糖数,
那么
Candy[i] = Candy[i-1]+1 if ratings[i] > ratings[i-1] 递增序列,后面小孩需要的糖果是前一个小孩的糖果数+1
1 if ratings[i] == ratings[i-1] 直线,按照题意,如果两个小孩rating一样多,后面的小孩可以只拿一个糖
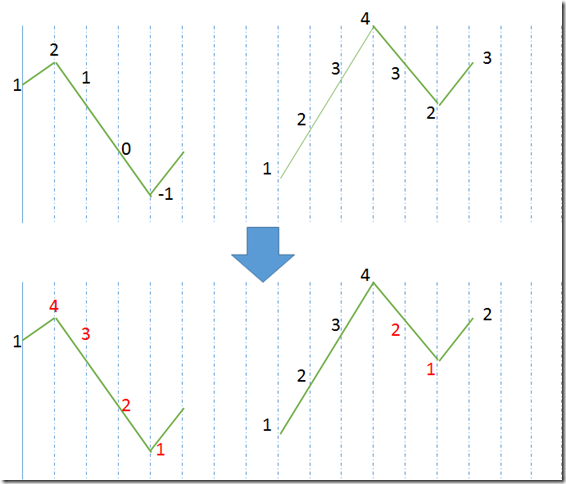
Candy[i-1] –1 if ratings[i] < ratings[i-1] 递减序列。这个递推式显然是有缺陷,因为如果递减序列比较长的话,Candy[i]就可能出现负值了,负值显然是没有意义的。比如下图为例:
蓝线是rating变化曲线,数字是Candy[i]的值。基于上面递推式的解(第一行)明显是不合理的。而第二行经过调整的(红色数字),才是最优解。简单的说,就是当遇到一个波谷的时候,调整一下左边的下降序列就好了,但是要注意区分条件,上一个波峰只在有些条件下才需要更改(例一和例二的区别)。
[Code]
1: int candy(vector<int> &ratings) {
2: vector<int> candy(ratings.size());
3: candy[0] = 1;
4: int i =1;
5: for (; i < ratings.size(); ++i)
6: {
7: if (ratings[i] > ratings[i-1]) //递增
8: {
9: candy[i] = candy[i - 1] + 1;
10: }
11: if (ratings[i] == ratings[i-1]) //平行
12: {
13: candy[i] = 1;
14: }
15: if (ratings[i] < ratings[i - 1]) //递减
16: {
17: candy[i] = candy[i - 1] - 1;
18: }
19: if (i<ratings.size()-1 && ratings[i] < ratings[i-1] && ratings[i] <=ratings[i+1])
20: ReAdjustCandy(ratings, candy, i);
21: }
22: if (ratings[i-1] < ratings[i-2])
23: ReAdjustCandy(ratings, candy, ratings.size() - 1);
24: int total = 0;
25: std::for_each(candy.begin(), candy.end(), [&](int n){
26: total += n;
27: });
28: return total;
29: }
30: void ReAdjustCandy(vector<int>& ratings, vector<int>& candy, int startIndex)
31: {
32: int k = startIndex;
33: int diff = 1 - candy[k];
34: while (k > 0 && ratings[k - 1] > ratings[k])
35: {
36: candy[k] = candy[k] + diff;
37: k--;
38: }
39: if (diff > 0) candy[k] += diff;
40: }