In Binary Tree, Inorder successor of a node is the next node in Inorder traversal of the Binary Tree. Inorder Successor is NULL for the last node in Inoorder traversal.
In Binary Search Tree, Inorder Successor of an input node can also be defined as the node with the smallest key greater than the key of input node. So, it is sometimes important to find next node in sorted order.
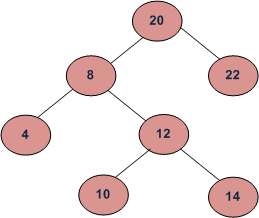
In the above diagram, inorder successor of 8 is 10, inorder successor of 10 is 12 and inorder successor of 14 is 20.
Method 1 (Uses Parent Pointer)
In this method, we assume that every node has parent pointer.
The Algorithm is divided into two cases on the basis of right subtree of the input node being empty or not.
Input: node, root // node is the node whose Inorder successor is needed.
output: succ // succ is Inorder successor of node.
1) If right subtree of node is not NULL, then succ lies in right subtree. Do following.
Go to right subtree and return the node with minimum key value in right subtree.
2) If right sbtree of node is NULL, then succ is one of the ancestors. Do following.
Travel up using the parent pointer until you see a node which is left child of it’s parent. The parent of such a node is the succ.
Implementation
Note that the function to find InOrder Successor is highlighted (with gray background) in below code.
1: #include <stdio.h>
2: #include <stdlib.h>
3: /* A binary tree node has data, pointer to left child
4: and a pointer to right child */
5: struct node
6: {
7: int data;
8: struct node* left;
9: struct node* right;
10: struct node* parent;
11: };
12: struct node * minValue(struct node* node);
13: struct node * inOrderSuccessor(struct node *root, struct node *n)
14: {
15: // step 1 of the above algorithm
16: if( n->right != NULL )
17: return minValue(n->right);
18: // step 2 of the above algorithm
19: struct node *p = n->parent;
20: while(p != NULL && n == p->right)
21: {
22: n = p;
23: p = p->parent;
24: }
25: return p;
26: }
27: /* Given a non-empty binary search tree, return the minimum data
28: value found in that tree. Note that the entire tree does not need
29: to be searched. */
30: struct node * minValue(struct node* node) {
31: struct node* current = node;
32: /* loop down to find the leftmost leaf */
33: while (current->left != NULL) {
34: current = current->left;
35: }
36: return current;
37: }
Method 2 (Don't Use Parent Pointer)
Inorder travel the tree and
1) If current visit node is target node, mark the indicator as true.
2) If indicator is true, print the node and return.
Implementation
1: struct node * inOrderSuccessor(struct node *n, struct node* target, bool& indicator)
2: {
3: if( n== NULL )
4: return NULL;
5: if(indicator) return n;
6: if(n == target) { indicator = true; return;}
7: node* left = inOrderSuccessor(n->left, target, indicator);
8: node * right =inOrderSuccessor(n->right, target, indicator);
9: if(left != NULL) return left;
10: if(right!= NULL) return right;
11: return NULL;
12: }