[HNOI2004]敲砖块

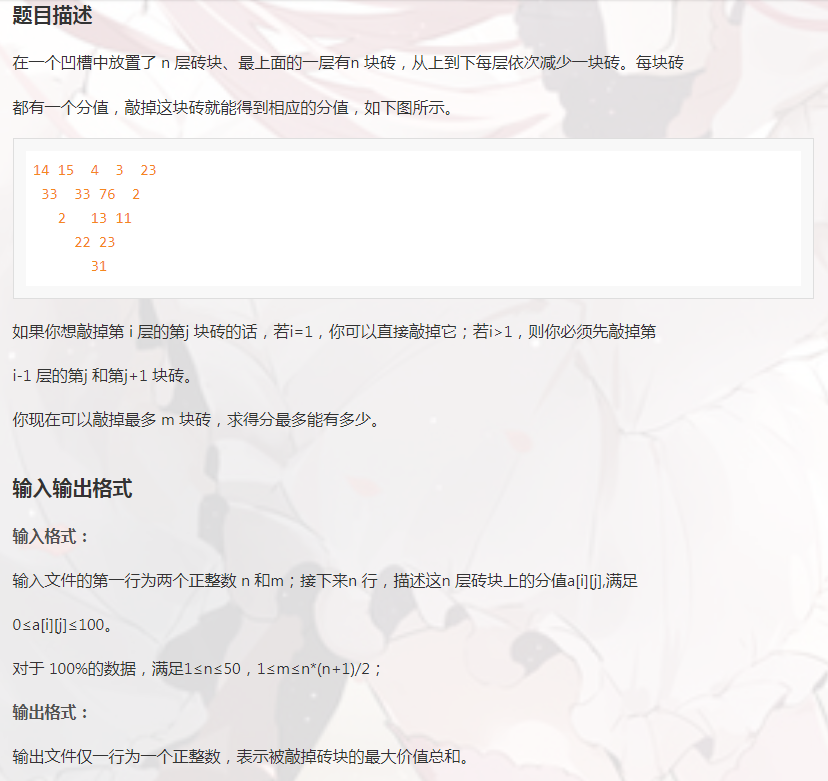
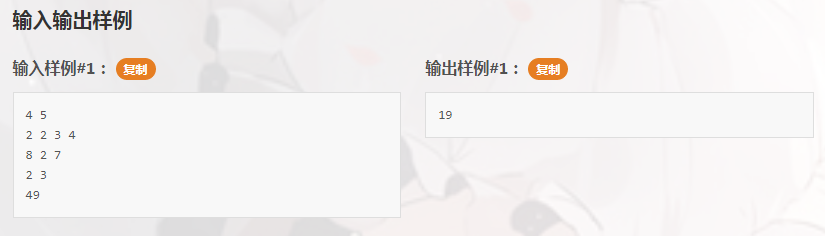
 直接用题目中三角形

我们发现无论是从上到下还是从下到上DP都会有后效性

这时我们发现第i列的情况只和第i+1列有关

于是我们产生了从右向左DP的思路

到这为止我的想法，就开始与别人不同了

我用f[i][j][k]表示，敲掉第i行第j列的那个块，和之前的k-1个块所能得到的最大分数

用ji[j][[k]表示，当前列的前一列j-n列敲掉k个块所能得到的最大分数

用滚动数组变为ji[k]方便书写

转移的话就拿f[j][i][k]=max(ji[k-j]+s[j][i],f[j][i][k]);来转移

但注意要特殊处理j=0的情况

for(int k=0;k<=m;k++) f[0][i][k]=ji[k];

总的来说此题细节极多，较好的DP题

实现如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <map>
#include <cstdlib>
#include <algorithm>
#include <queue>
#include <stack>
#include <vector> 
using namespace std;
inline int read()
{
    register int a(0),p(1);register char ch=0;
    while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
    if(ch=='-') p=-1;
    while(ch>='0'&&ch<='9')a=a*10+ch-48,ch=getchar();
    return a*p;
}
const int N=60,M=2010;
int n,m,a[N][N],s[N][N],f[N][N][M],ji[M],ans=0;
int main()
{
    // freopen("input","r",stdin);
    // freopen("output","w",stdout);
    n=read(),m=read();
    for(int i=1;i<=n;i++) for(int j=n;j>=i;j--) a[i][j]=read();
    for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) s[j][i]=s[j-1][i]+a[j][i];
    memset(f,-1,sizeof(f));
    for(int i=0;i<=n;i++) for(int j=0;j<=m;j++) f[0][i][j]=0;
    for(int i=1;i<=n;i++)
    {
        memset(ji,0,sizeof(ji));
        for(int j=i;j>=1;j--)
        {
            for(int k=0;k<=m;k++) ji[k]=max(ji[k],f[j-1][i-1][k]);
            for(int k=j;k<=m;k++)
                if(f[j-1][i-1][k-j]!=-1)
                {
                    f[j][i][k]=max(ji[k-j]+s[j][i],f[j][i][k]);
                    ans=max(ans,f[j][i][k]);
                }
        }
        for(int k=0;k<=m;k++) f[0][i][k]=ji[k];
    }
    printf("%d",ans);
    return 0;
}