还是之前的问题,求出MAXSIZE以内的所以质数
下面我们看下原理
所有的合数都可以分解为两个数的乘积,那么我们建立一个isPrime[MAXSIZE+1]的表,先把所有的元素设置成默认为是质数,true,设置两重循环,将i*j处的值设置成false,这样最后得到的是true元素对应的角标就是质数了,下面附上代码:
#include <iostream> #include <time.h> using namespace std; #define max 99999 int prime[max+1]; bool isPrime[max+1]; int count = 0; int main() { for (int i = 0;i <= max;i++) { prime[i] = 0; isPrime[i] = true; } clock_t start,end;//用于计时 start = clock() ; for (int i = 2;i <= max;i++) { for(int j = 2;j <= max && i*j <= max;j++) { isPrime[i*j] = false; } } end = clock(); for(int i = 2;i <= max;i++) { if (isPrime[i]) { cout<<i<<" "; } } cout<<" 总共花费了"<<(long double)(end - start)/CLOCKS_PER_SEC<<"秒"<<endl; return 0; }
这里我们可以看到,其实没有经过什么优化,让我们看戏程序的效率:
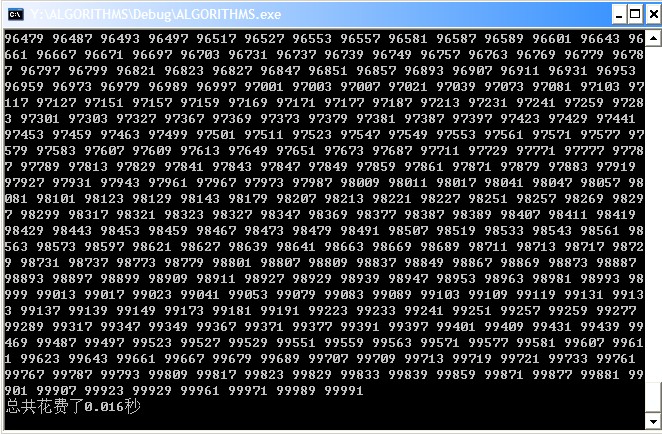
这个效率已经很高很高了,比之前的筛选法还要高了,下面我们看下在这个算法中还能怎么样去减少循环次数,减小程序的时间复杂度
设想下,在2*4 = 8处和4*2 = 8处,或者 2* 12 = 24和3*8 = 24处,都分别进行了多次赋值,这样看来,效率有所降低,下面是我们优化过的代码,

#include <iostream> #include <time.h> using namespace std; #define max 99999 int prime[max+1]; bool isPrime[max+1]; int count = 0; int main() { //将数组初始化 for (int i = 0;i <= max;i++) { prime[i] = 0; isPrime[i] = true; } clock_t start,end;//用于计时 start = clock() ; for (int i = 2;i <= max;i++) { if (isPrime[i]) { prime[count++] = i; } for(int j = 0;j < count && i*prime[j] <= max;j++) { isPrime[i*prime[j]] = false; if (i % prime[j] == 0) { break; } } } end = clock(); for(int i = 2;i <= max;i++) { if (isPrime[i]) { cout<<i<<" "; } } cout<<" 总共花费了"<<(long double)(end - start)/CLOCKS_PER_SEC<<"秒"<<endl; return 0; }
通过prime数组保存已经得到的质数,然后用这些质数去乘以i得到合数,并将该合数对应的位置置为false,关键还有一个
if (i % prime[j] == 0) { break; }
操作,比如,当i为8的时候,搜索到2,也就是2*8 = 16,处置为false就可以了,跳出J的循环,因为假如到8*3=24的话 24 = 2*12,可以由一个更大的合数得到,这样就可以减少循环次数,优化时间复杂度,下面看程序运行结果:
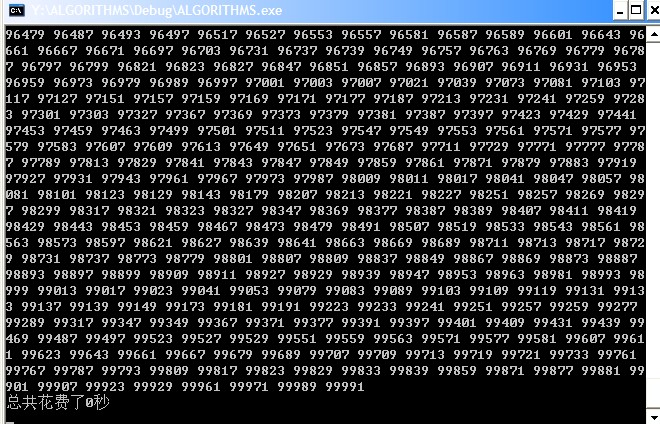
这个时间,你懂的!
