排序算法是最为常用的基础算法之一。排序是数值计算基础,本节将着重于高效的内排序算法。分治法作为排序中较为重要的思想,核心在于“分而治之,各个击破”。
一般情况下的思想是通过两两比较进行排序,实际产品环境中采用两两比较虽然理论上可以解决现实问题,但是实际上却不会采用两两比较的方式,因此本节中将会介绍性能较高的排序算法,也是实际中用得最多的方式。
一、快速排序
快速排序(Quick Sort)采用分治法的思想,把一个数值序列划分为两个子序列,然后对两个子序列再进行分治法的思想。计算过程如下:
- 从数值队列中选择一个基准元素。
- 将队列中的其它元素与基准元素比较,比基准元素小的元素放在基准元素的左边,比基准元素大的元素放在右边(降序排列则相反),则队列被基准元素划分为左右两个区间。
- 对两个区间的值,分别递归步骤2,使得最终形成有序的序列。
虽然上述步骤采用的是递归的方式,但是当区间小于等于1时,将会直接返回,因此不会无限制递归下去。例如对于队列数值“4 3 6 2 5”采用快速排序进行升序排列过程如下图所示。

如上图所示,以数值“4”为基准,将比其小的元素“3”、“2”放置到左边,比其大的元素“6”、“5”放置到右边,形成以4为基准的左区间和右区间,然后对左区间和右区间分别再次选择出基准元素,重复上述过程,最终得到数值序列“2 3 4 5 6”。
- 时间复杂度。最坏的时间复杂度
,最优的时间复杂度
,平均时间复杂度
。
- 空间复杂度。快速排序的空间复杂度相对而言依然与具体的实现有关。
二、归并排序
归并排序(Merge Sort)是指将两个已经有序的序列合并成一个有序序列的排序方式。归并排序可以采用迭代的方式进行排序,例如有两组数值序列A、B,采用归并排序进行升序排序,则排序步骤如下所示:
- 申请存放最终合并后的数值序列存放空间,空间大小为数值序列A、B的空间之和。
- 初始化两个指针,分别指向数值序列A、B的首元素地址。
- 比较两个指针对应的值,将较小的值放入到最终存放空间,并移动较小值指针到序列的下一位。
- 重复上一个步骤,直到某一个指针已经指到序列的队尾,已经没有元素和另外一个序列进行比较。
- 将另外一个序列的剩余元素直接拷贝到最终序列存放空间的末尾。
采用的两组数值序列A、B,可以采用递归的思想,将一个大的序列拆分为两组子序列,然后对两组子序列再次进行拆分,直到每一个子序列中仅有一个元素,然后将两个只有一个元素的序列归并为一个含有两个元素的序列,再将两个含有两个元素的序列进行归并,依此类推,直到所有元素都完成归并,如下图所示。

- 时间复杂度。归并排序的最差时间复杂度
,最优时间复杂度
,平均时间复杂度
。
- 空间复杂度。归并排序的空间复杂度与具体实现相关,最差空间复杂度不应高于
。
三、堆排序
堆排序(Heap Sort)是基于堆的数据结构而实现的排序算法。堆是一种日常中使用较多的数据结构,对于含有N个数值序列的 ,若满足
小于等于
且
小于等于(大于等于)
(其中1≦i≦n/2)则可以被称小根堆,小跟堆是堆顶的元素值是堆里所有元素节点中最小的值;相反,当
大于等于
且
大于等于
,即堆顶的元素值是堆里所有结点关键字中最大的堆被称作大根堆。
根据上述描述的堆性质,最小堆的第0个元素是整个堆中的最小值,最大堆的第0个元素是整个堆中的最大值。
由于堆的堆顶元素是最大值或最小值,因此可以利用此特性,每次从数组中可以直接选取出最大值或者最小值,使得每次排序变得相对简单。堆排序的实现步骤分为下列四步。
- 将初始元素值
构建大顶堆(最大堆)。
- 将堆顶元素
与最后一个元素
置换,此时可将所有排序元素区分为两个部分,其中置换后的
属于有序集合,前序元素
属于无序集合。
- 根据第二步结果,将无序集合中的元素再次进行大顶堆调整,将得到的堆顶元素与最后
置换,得到有序集合
以及无序集合
。
- 重复上述过程直到无序集合中的数据小于2,然后将有序集合与无序集合的最后一个元素合并,最终得到完整的有序集合。
排序元素的升序排序或降序排序,取决于排序过程采用的是最小堆结构还是最大堆结构。以给定数组a[6] = {18,8,5,39,20,10}为例,进行构建堆的示例。
- 首先将a数组中的元素构建一棵完全二叉树,如下图所示。
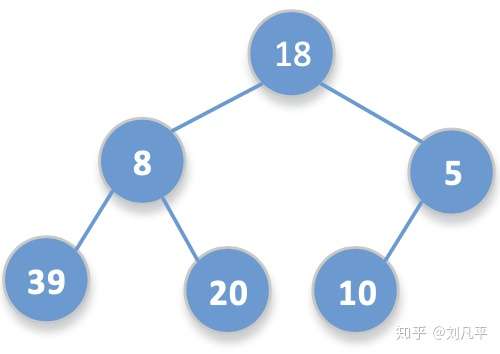
2. 构建初始堆。初始堆的构建过程则是从最后一个非叶子节点开始,即元素5开始,调整过程如下图所示。

3. 重复迭代进行堆排序。
通过上图所示的初始堆,则已经将整个元素集合中最大的元素39找到。因此将元素值39纳入到有序集合中,再次对剩余的无序集合进行构建最大堆,不断迭代,最终获得的有序集合元素即是由大到小的排序结果。
通过上述过程可以发现堆排序的过程实质也是一种选择性排序,它借助了数据结构的树形结构进行排序。在性能方面,堆排序的最坏时间复杂度为 ,最优时间复杂度为
、平均时间复杂度为
、最差空间复杂度为
。
四、基数排序
基数排序(Radix Sort)的原理是将数值按照位数进行切分为不同数字,然后对每一位数分别进行比较从而达到排序的目的,可以通过以下三个步骤完成。
- 将所有需要进行比较的数值序列统一为相同长度的位数,如果位数较短的数值,则在最前面补充0。
- 从位数的最低位开始,依次进行排序,得到初步的排序结果。
- 在上一步的排序基础上,从次低位继续开始依次进行排序后,得到新的排序结果。
- 重复2~3步骤,从低位向高位进行排序,最终得到完整有序的序列。
基于位的重复迭代的过程是基础排序的重要思想,例如对数组a[5]={14,27,5,100,19}利用基数排序进行升序排序如下步骤所示:
- 首先按照个位数进行排序,得到结果:100、14、5、27、19。
- 其次按照十位数进行排序,得到结果:5、100、14、19、27。
- 最后依据百位数进行排序,得到最终有序的结果:5、14、19、27、100。
采用基数排序进行排序时,需要注意负数的情况,并且下一次的排序依赖于上一次的排序结果。从性能方面而言,基数排序最差时间复杂度为 ,最差空间复杂度为
,其中n是元素的个数,
是数值的位数,
值决定了需要进度多少轮处理。
五、外排序
前面介绍的快速排序、归并排序、基数排序等都属于内排序,内排序是指能够在内存中完成的排序方式。当计算机内存小于数据本身大小时,无法一次性将数据加载到内存,这个时候则需要采用外排序的方式。
外排序主要是针对大文件的排序,将需要排序的数据文件存放到存储器中,每次加载部分数据到内存,不断进行内存和外部存储器之间的数据交换,最终保证文件中的每个数据都完成排序。
例如有4G的数据文件需要进行排序,当前操作系统的有效可用内存为1G(不考虑其它内存消耗),则需要按照外归并排序的流程完成排序,步骤如下:
- 将4G的数据文件,平均拆分为1G的数据文件。
- 将每一份1G数据文件加载到内存,采用内排序的方式(可以是快速排序、堆排序、基数排序等的任意一种内排序)在内存中完成对该数据文件的排序,并将排序后的结果写入到文件。
- 然后采用四路归并的方式进行归并排序,在4个1G文件中,分别读取200M数据存入内存的输入缓冲区,共占用计算内存800M,将剩余的200M作为输出缓冲区,如下图所示。

4. 将输入缓冲区的四路数据进行归并排序,依次存入到输出缓冲区,当输出缓冲区满时,则写入到文件,当输入缓冲区中某路数据完毕之后,再向文件中读取200M数据到输入缓冲区,不断进行该过程直到所有的数据通过四路归并的方式完成排序。
在外排序中,外归并排序是最常用的方式。在上例中,采用了四路归并方式,同理还有二路归并排序、三路归并排序、多路归并排序等等。它们的共同特征在于将内存分为输入缓冲区和输出缓冲区,在输入缓冲区中加载已经有序的集合,在输出缓冲区进行归并排序,然后将输出缓冲区写入文件;不同点在于输入缓冲区数据的路数不同。
由于外排序需要在内存和存储器之间不断进行数据调度,所以它的性能相对也会较内排序更加依赖于硬件,因此若是要增强外排序的性能,可以通过以下方式改进部分处理性能:
- 采用多个磁盘驱动器并行的处理数据,可以加快磁盘的读写速度。
- 采用SSD固态硬盘的方式读取数据,机械硬盘的读写速度相对而言远远小于SSD固态硬盘。
- 程序可以采用多线程的方式进行数据读写。
- 采用多核、高频的CPU处理器也可以得到一定的优化。
- 程序分布式化,将程序部署于分布式计算平台。
此外,增加内存是最直接的改善外排序性能的方式,但是目前实际应用而言,数据的大小一般都远远大于计算机的内存,因此只能起到缓解作用,抛离硬件的因素,数据处理过程的并行化与分布式化是主要的改进方式。