模型构建
·[529]|1000天行动计划
读书笔记/热点追踪/论文研读/教程手册
继续建模过程,上节主要是建模的初步处理,本节开始建模型的有关具体操作。
首先,对于模型有前处理和后处理的过程,所谓的前后实际上是以模型的运行为参照的,前就是模型的运行前的处理,模型后处理就是模型运行后的处理。所以,前处理过程也就是我们现在的建模过程。
网格划分
网格划分是建模的第一步,对于非零维模型,都需要建立网格。网格的含义,在之前的文章中有叙述,可查看网格 网格2文章。这里简单谈谈我的看法,划分网格的主要是因为计算的需要,因为水质模型底层的物理规律是基于多个微分方程的,如N-S方程,但这些方程式并不是所有都能求解解析解的,那么牺牲精度换得能计算,跟我们一直强调的『先求其有,后求其美』一样,采用数值计算的方法进行近似求解。当然,数值计算的方法有多种,如有限差分法、有限体积法等,但是不管哪种方法,都需要将研究对象离散化,也就是划分相应的网格。
另外,一种角度是在学习<地表水模型>时候想到的,Chapra先从零维模型开始切入,后介绍了正馈系统和反馈系统,即利用多个零维模型串联而成,明确多个零维之间的关系,联立即可构成最简单的一维模型。所以,所谓的网格化可以理解为多个零维的简单模型有机组合起来表达了空间上的变化。
网格的划分针对不同的水质模型,有不同的划分方法,商业类软件比较友好,目前都有较为成熟的工具,开源模型就比较麻烦点,一般需要借助其他工具,这点往往成为新手的拦路虎,所以建议大家一开始学从商业模型入门比较好。好消息是现在讲究开源,有很多的开源算法能够很容易的生成网格,坏消息是生成的网格还需要根据模型的指定的格式去制作。
水质模型的网格目前主要有两大类:结构化网格和非结构化网格。结构化网格在计算方面有一定的优势,但是非结构化则对局部的研究对象的刻画比较方便,且整体比较容易绘制,其基本不需要技术含量,可以直接无脑生成,不用考虑结构网格中的贴边,正交之类的,也是未来的趋势,但是目前来看,水质模型领域结构网格仍然是主流。
这里贴一张delft3D官网的一张示例图:
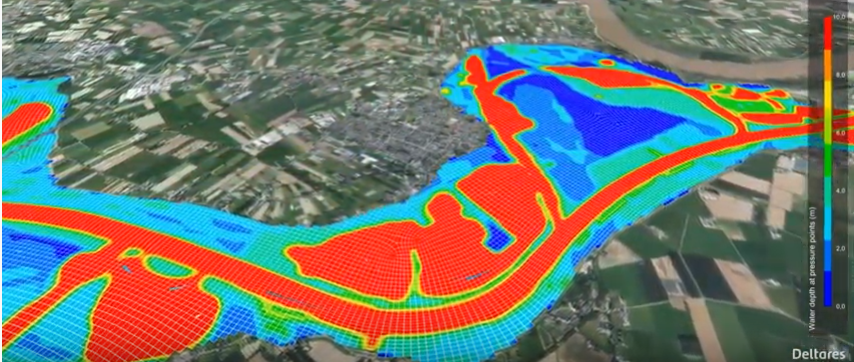
网格对应前面节提到的固壁边界,水平方向则是是网格最外围线来表达,而底边界则是由水下地形来表达,从而将研究对象完全隔离出来。一般情况下,只要表达清楚研究对象,到此就结束了,但是对于复杂的研究对象,网格的玩法就更为多样了。可能有以下问题需要关注:
- 内部区域有岛或者深沟。对于这些区域由于地形变化起伏大,在模型计算过程中容易出现发散,需要特别的处理。对于较大的岛屿来说,依据实际情况,可将网格挖去,直接将岛屿作为固壁边界。但是对于小一点的岛屿来说,其有可能会有水淹没或露出,那可以设置其实际的底部地形,采用干湿模式处理,什么是干湿模式呢,下面会说。但是一般情况我们还是尽量挖去,即让其不参与计算,不好处理,我就直接不处理了。而深沟和岛是相反的,其的问题是梯度的变化,也就是地形的变化太大,容易导致计算问题。
- 存在浅滩,可能部分时段是没有水的。这种情况对于宽阔的河流或者入海口比较常见,这些区域在水量较大时是处于有水状态,而在水量较小时,其处于滩地。那么,问题来了。我不可能像岛屿一样直接挖掉,那么我在有水的时候,本来是应该扩展到这些区域的水,由于没有网格,成了固壁边界,这些水就会壅高,与实际情况肯定不符,所以必须还是要用网格表达这些区域的,那么现在的问题就是这些网格如果没有水如何表达?方程求解是一视同仁的,并且计算的是水流这种物质,如果这个网格没有水,那么是无法进行计算的。那么就出现了干湿网格动态边界模式,所谓的干湿模式就是网格没有水的时候将其从计算中暂时除去,在有水时再变为湿网格继续计算,就解决了这个问题,当然这里与网格本身关系不大,而是一种计算模式的处理。
- 地形变化剧烈,有些河流上下游高差较大。学点数值计算对理解水质模型是有帮助的,因为你可以理解网格的平滑、正交究竟是为什么?对于地形变化剧烈的时候,需要进行一定的概化平滑操作,而对于河流的上下游高差,则需要注意其整体的坡度状态,模型内部方程的假设条件,能否适用这类问题。
- 内部或边界上存在水工构筑物。这类问题与岛屿类似之处,一方面可能需要对网格进行处理,网格线与这些贴合,使得其流场符合,另一方面可能需要根据模型本身的功能进行一些具体的处理。
边界条件输入
气象条件输入,气象从某种意义上也是边界条件的一种,如同网格表达了固壁边界一样,但是我们传统不将其称为边界条件。气象条件按格式输入即可,有关的气象的细节可能就是尽可能高频的连续数据,注意模型内部使用的单位即可。
水量、水质、水位等这类边界条件是驱动模型的边界条件,简称边界条件。边界条件,先说水质的边界条件,其在水质模型中通过两种方式,一种是负荷的方式,另外则是浓度的方式,本质是一样的。负荷相对来说是比较粗的形式,常见的是以浓度居多,因为存在不同的浓度和流量的组合。
再强调下,观测数据用于校准模型结果,而边界条件则为驱动模型运行的数据,主要是看数据如何使用。
首先,谈下动态模型的边界条件的时间序列,所谓的时间序列是由时间和值一起构成的数据列表,也就是数据具备时间属性,常见的如气温、降雨等数据,如下图所示为中央气象台的气象要素的时间序列图,图中的每个点都是一个数据。
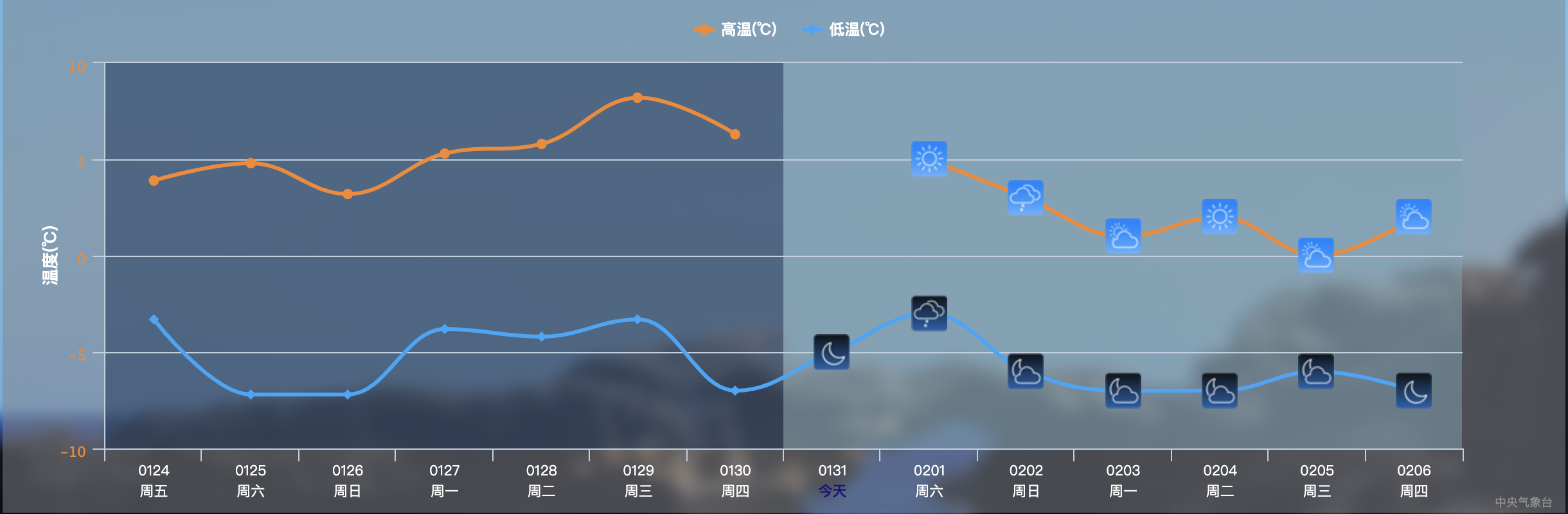
对于时间序列,时间频率非常重要,就是数据的时间间隔是多久一次的,间隔小时为小时尺度的数据,数据的频率对于模型来说影响非常大,不同的模型需求,需要的时间尺度不同,但是基本都是越高越好,毕竟高频数据能够降维为低频数据,低频数据不太好升维。
模型对于时间序列的使用,一般是会自动进行线性插值呢,简单的说就是上面的相邻的两个点的数据直接线性连接,两个时刻点中间的值就是线性计算出来的。这个主要是对于不同时间频率的数据混用时需要关注的,比如你的流量数据是小时尺度的,但是水质数据是日尺度的,两者作为模型的负荷输入时,这两套数据内部怎么使用的,就需要弄明白了。
水动力边界条件
那么,就说说几种常见的水动力边界条件。
- 流量边界。通过流量的方式输入到模型中,有恒定流量(恒定不变的流量)和流量时间序列(流量随时间变化),用于入湖河流、河流上游断面的来水,这比较容易理解,就不多解释了,需要注意的地方就是出流的流量边界可能是以负数表达,或模型自己规定的方式。另外,对于具体模型设置方面,对于流量边界的实际设置,需要注意多个网格的流量分配问题,之所以分配,一方面是要匹配实际情况,另外也为了计算上的稳定,比如具体而言如河流横断面有多个网格,则多个断面网格上进行流量的分配(对于宽的河流,其整个横断面上并不一定是均匀的流量);而深度方向考虑,多层的网格,存在垂向分配的问题,就是表层流速快的情况,对于湖泊呢,入湖河流流量大的时候也可分配到多个网格上(因为网格分辨率并不一定就是等于入湖河流宽度)。
- 水位边界条件。给定的水位随时间变化的序列,直白点说就是设置某位置的水位为给定的值,这种水位边界用在河流或者海洋的开边界上,因为其的“能量”非常的强大,且多用于下游(外海)位置处,实际使用时务必注意这种边界有可能会引起一定的回流,那么与之匹配的水质边界就需要设置的比较合理,否则会出现很多问题,对于有回流的可以考虑。
- 水位——流量边界。这是一种通过水位——流量的关系确定的一种边界条件,输入这种边界后,模型会通过边界位置处的网格的实际水位来确定其出网格的流量,对于一般的河流,这种水位-流量边界条件更加的合理,因为这种边界条件是单向的,不会有回流产生,而水位边界条件是可能有回流的,同时对于湖泊出口一般是闸控或者溢流坝的,溢流坝的本质就是水位——流量关系,水位到达一定值,其按照一定的流量出流,所以这种边界条件也是应用十分的广泛,这个和上述的水位边界的特征不一样,要注意区分。
水质边界条件
对于水质模型而言,水动力边界条件仅仅是模拟水动力模型,水质模型需要有水质边界条件,水质边界相对来说比较单一。一般为浓度边界,当然也有负荷边界,但是两者没有本质都不同,其最终都为往系统中输入负荷。对于浓度边界,一般多与水动力的流量边界边界配合使用,通过流量与浓度的组合来进行实现负荷的输入。
水质边界需要强调的是输入的水质指标和指标的单位。这个需要根据模型所描述的量进行具体的匹配。指标的名称和单位一定要反复确认,这个非常的重要,很容易出现牛头不对马嘴的错误,我们都知道汽车加油要有对应的型号,如果加错了,轻则动力不足,重则发动机损坏,所以务必注意。
大家需要根据具体的模型,仔细核对说明书。现在仅仅根据自己的经验,举几个简单的例子,以EFDC为例,水质指标的问题,最常见的一个错误就是其中的COD,模型中的COD表达的是仅仅甲烷等无机物消耗的氧气量,而非国内的化学需氧量,看到一些同学拿这个COD去模拟化学需氧量,不管你模型设置的多么好,校准的多么好,不好意思,都是错的。
单位方面呢,一个坑就是叶绿素a了,对于叶绿素a的单位,我们通常用的都是ug/L,但是对于efdc模型而言,其并非直接模拟叶绿素a的,而是通过生物量来进行模拟,其是以 碳 计量的,对于水质边界条件的输入单位是 mg C/L,所以输入模型时,必须输入是转化为碳计的量。
初始条件
水动力和水质的初始条件的设置基本类似,将模型模拟开始时刻的数据输入模型作为模型运行开始时刻的初始场。比如,对于河流的模拟,从2020年1月1日,0:00开始的模拟,你需要输入这个时刻河流所有的状态,模拟区域所有位置的水位、水温、水质指标浓度,甚至还有流场的情况(位置通过网格来体现),对于湖泊也是一样的。单纯考虑模型的初始条件,假设模型的边界条件是正确的,参数也是正确的。那么输入初始条件后,模型在边界条件驱动下开始运行,模拟的结果就即刻开始可以使用了,代表了真实的结果。
这个是理想情况,你也知道这个显然是不可能的,根本就没法获得上述的初始条件,那么我们究竟要怎么办?
先从模型的机理角度来看,初始条件在经过多个时间步长后,其的作用在模型中会逐渐“消失”,换句话说,不管设置的初始条件是什么样,经过足够长的时间后,其对该时段的模拟的影响都会消失。从这个角度来看,我们根本就没有必要设置初始条件了,随便设置一个就可以了。
那我们还为什么要设置初始条件呢?理由就是前面的足够长,如果设置的是正确完全的初始条件,这个足够长实际上几乎就是0了,就是上面的理想情况。那么我们如果输入的是完全错误的(这个当然是为了便于理解举例而举例),那么这个足够长就是无限长。
那输入有限的初始条件,需要的时间就介于0~无限长之间了。我们称这个时段为热身时间,热身时间有如下特点:热身时间内的模拟结果是无效的;真实的初始条件,热身时间=0。
输入的初始信息越接近真实情况,那么热身的时间就越短,我们无法获取到真实完备的初始条件,但是能够输入足够多的初始信息的话,就能使得热身时间足够短。这个时间短有什么用呢?比如你只有两年的数据,如果热身的时间为一年,那么模型有效的结果只有一年了。
有关这个热身时间,水动力和水质的热身时间不同,水动力的范围几小时到几百天不等,水质的一般都需要数月。所以水动力的初始条件可以随意一些,而水质的初始条件就需要尽量的设置好。此外,不同类型的模拟对象,热身时间也不相同,河流的一般要短于湖泊,这个与水动力条件、内部动力过程等相关。
热身实际上在水质模型中有专业的术语,有关Cold start(冷启动)和Hot start(热启动),就是说这个的,具体的这里不深入阐述了。
回过头来说初始条件的信息,初始条件是一个场,但是往往没有那么多的数据,那么其需要进行空间的插值,具体的插值的影响也会影响热身时间,但是这个并不是关注的重点,因为其插值本身并没有引入有效的信息。
对于场也有例外,就是在湖泊中的水位,湖泊较小时其湖面是水平面,所以其直接均匀场,不过均匀场也是一种特殊的场。
小结:
在上述所有条件设置完毕之后,模型已经有了基本的框架了,模型就可以运行计算了。
到此模型的基本建模已经完成,这里忽略了一些过程的设置,如模型模拟的物理过程选择,是否模拟风、盐的作用,因为不同的模型有所不同,不能一概而论。
那么,从上述过程可以看出,模型的建模过程如同搭建积木,逐步的将各个模块组合起来,最后形成了整个模型,后续缺少什么还能进行细节的完善,但是基本的框架基本不会变了,整个建模并不复杂,只要数据足够,建模过程非常的容易,理解了基本的概念之后,按照通用的步骤去操作即可。
到目前,如果上述能够看懂了,那么对于大部分的水质模型的论文已经能够看懂了。手头有一份网络上下载的Delft3D水质模型建模报告,入群即可下载学习。
由于教程系列文章需要花费很多时间,难免出错,而这里不能进行后续完善,所以推荐大家关注我的博客,获取最新的修正和补充。 公众号的社群同步开启,感兴趣可在公众号对话框回复“社群”,获取群号和加入方式。

微信公众号 | 水环境编Cheng长 网 站 | comieswater.com
2019-11-27
folder=/微信公众号/水环境编Cheng长/