1. 题目信息
附件给出实现流加密的Python脚本与一段输出的密钥流。
2. 分析
通过对加密脚本的理解,可得本题的LFSR模型:
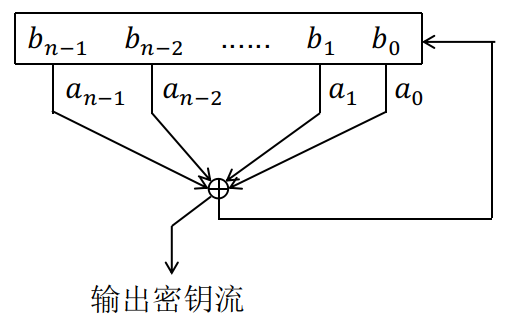
其中 (a_{n-1},a_{n-2},cdots,a_0) 为程序中 mask 的二进制位,当 (a_i=1) 时,将 (b_i) 输入异或运算,否则 (b_i) 不输入异或运算;根据模型我们可以得到如下等式:
[egin{pmatrix}
k_{1} \
k_{2} \
vdots \
k_{n-1} \
k_{n} \
end{pmatrix}=egin{pmatrix}
b_{n-1} & b_{n-2} & cdots & b_{1} & b_{0} \
b_{n-2} & b_{n-3} & cdots & b_{0} & k_{1} \
vdots & vdots & ddots & vdots & vdots \
b_{1} & b_{0} & cdots & k_{n-3}&k_{n-2} \
b_{0} & k_{1} & cdots & k_{n-2}&k_{n-1} \
end{pmatrix}cdot egin{pmatrix}
a_{n-1} \
a_{n-2} \
vdots \
a_{1} \
a_{0} \
end{pmatrix}
]
其中的加法为异或,因为(a_{n-1} =1),将上式重写如下:
[egin{pmatrix}
k_{1} \
k_{2} \
vdots \
k_{n-1} \
k_{n} \
end{pmatrix}=egin{pmatrix}
b_{n-1} \
b_{n-2} \
vdots \
b_{1} \
b_{0} \
end{pmatrix}oplus egin{pmatrix}
b_{n-2} & cdots & b_{1} & b_{0} \
b_{n-3} & cdots & b_{0} & k_{1} \
vdots & ddots & vdots & vdots \
b_{0} & cdots & k_{n-3}&k_{n-2} \
k_{1} & cdots & k_{n-2}&k_{n-1} \
end{pmatrix}cdot egin{pmatrix}
a_{n-2} \
a_{n-3} \
vdots \
a_{1} \
a_{0} \
end{pmatrix}
]
由异或性质:
[egin{pmatrix}
b_{n-1} \
b_{n-2} \
vdots \
b_{1} \
b_{0} \
end{pmatrix}=egin{pmatrix}
k_{1} \
k_{2} \
vdots \
k_{n-1} \
k_{n} \
end{pmatrix}oplus egin{pmatrix}
b_{n-2} & cdots & b_{1} & b_{0} \
b_{n-3} & cdots & b_{0} & k_{1} \
vdots & ddots & vdots & vdots \
b_{0} & cdots & k_{n-3}&k_{n-2} \
k_{1} & cdots & k_{n-2}&k_{n-1} \
end{pmatrix}cdot egin{pmatrix}
a_{n-2} \
a_{n-3} \
vdots \
a_{1} \
a_{0} \
end{pmatrix}
]
再将等式“还原”:
[egin{pmatrix}
b_{n-1} \
b_{n-2} \
vdots \
b_{1} \
b_{0} \
end{pmatrix}=egin{pmatrix}
k_{1} & b_{n-2} & cdots & b_{1} & b_{0} \
k_{2} & b_{n-3} & cdots & b_{0} & k_{1} \
vdots & vdots & ddots & vdots & vdots \
k_{n-1} & b_{0} & cdots & k_{n-3}&k_{n-2} \
k_{n} & k_{1} & cdots & k_{n-2}&k_{n-1} \
end{pmatrix}cdot egin{pmatrix}
a_{n-1} \
a_{n-2} \
vdots \
a_{1} \
a_{0} \
end{pmatrix}
]
计算的顺序由下至上,即可解出初始状态的所有比特位。
3. 解题
实现的Python脚本如下:
from gmpy2 import c_div
def lfsr(R,mask):
output = (R << 1) & 0xffffff
i=(R&mask)&0xffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
def cal(s,mask):
lm=len(bin(mask))-2
R=int(s[-1:]+s[:-1],2)
ss=''
for j in range(lm,0,-1):
(_,tk)=lfsr(R,mask)
ss=str(tk)+ss
R=int(s[j-2]+str(tk)+bin(R)[2:].rjust(lm,'0')[1:-1],2)
return ss
def solve():
mask=0b1010011000100011100
lm=len(bin(mask))-2
with open('key','rb') as f:
stream=f.read(c_div(lm,8))
s=''.join([bin(256+ord(it))[3:] for it in stream])
flag='flag{'+cal(s[:lm],mask)+'}'
return flag
if __name__=='__main__':
print solve()
程序运行结果如下:
$ python solve.py
flag{1110101100001101011}