格林公式:
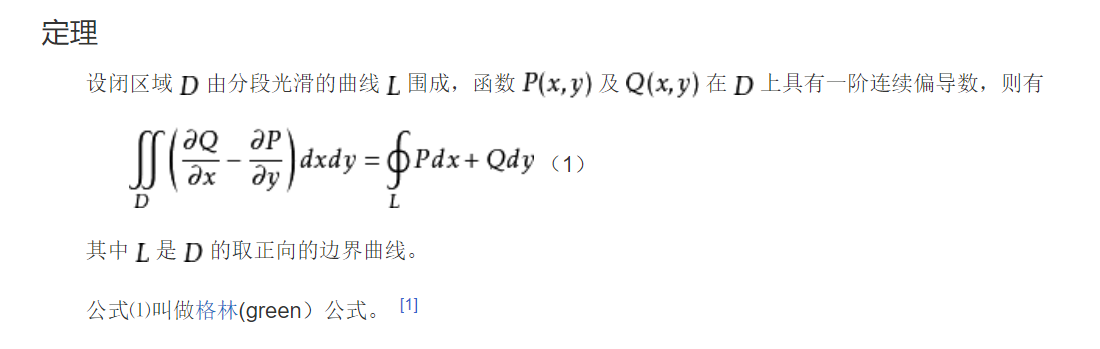
正向边界曲线:
当xOy平面上的曲线起点与终点重合时,则称曲线为闭曲线。设平面的闭曲线L围成平面区域D,并规定当一个人沿闭曲线L环行时,区域D总是位于此人的左侧,称此人行走方向为曲线L关于区域D的正方向,反之为负方向。
如果不为正向曲线,把对曲线的积分化为二重积分时,要在二重积分前面加一个负号。
高斯公式:

如果曲面为内侧,加一个负号。
只有对面积的曲面积分(dS)才有对称性。对坐标的积分不能用(如dxdy)
用高斯公式的时候可能是:题目为pdydz+qdxdz+...的形式,用高斯公式转化为∭(***)dV的形式,然后算体积或者用柱坐标。
三重积分的柱坐标计算方法,p,o范围由Dxy确定,z的范围:用平行与z轴的直线穿过该闭区域来确定
梯度
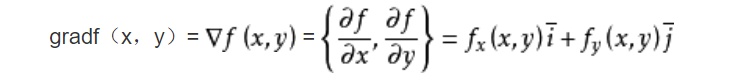
就是求偏导后结果组成的向量
与方向导数的关系:

意思是任取一个向量,当这个向量取的方向和梯度方向一样的时候,该向量方向上的方向导数最大,为梯度的模
关于二重积分的对称问题:
有函数f(x,y),积分区域D关于x对称,且改变y的正负号,f(x,y)函数值相同(积分值的正负只取决与背脊函数的政府)。
那么该函数在D的积分值等于在该函数在D1(y>=0或者y=0)的部分。
关于背脊函数为绝对值函数:
应该会用到对称性,但是用了对称性后f((x,y),不能发生变化,所以药转化到去掉绝对值表达式一样的区域(正区域)
关于平移:

可以把根号那一部分看成一个半圆,然后做平移变换(表达式里为y,则是对x进行变换,在x外面+右-左)
相同函数的积分在不同区域的积分,其积分域要取并集(可以从面积角度理解)