机器学习——聚类分析和主成分分析
在机器学习中,非监督性学习主要用来分类。其中重要的两种就是聚类分析和主成分分析。这两类算法在数据压缩和数据可视化方面有着广泛的应用。
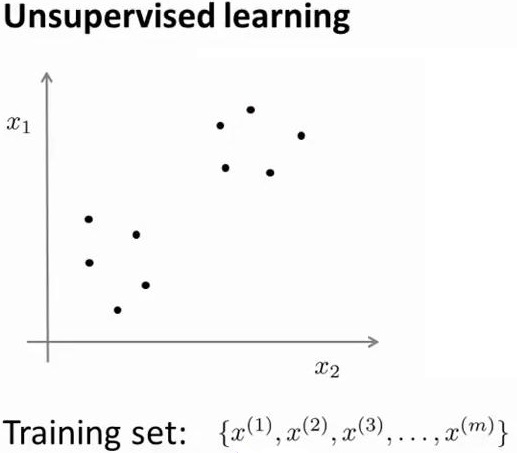
所谓无监督学习是指训练集里面只有点({x^{(1)},x^{(2)},ldots,x^{(m)}}),没有对应的性质标签(y)。所以非监督性学习的目的不再是预测,而是分类。
一、聚类分析
经典的聚类分析算法是K-mean算法。K是类的数目,mean是均值。
1. K-mean算法
- 1.给定训练集({x^{(1)},x^{(2)},ldots,x^{(m)}},x^{(i)} in R^n),随机选取(k)个聚类的质心点,记为(u_1,u_2,ldots,u_k in R^n)
- 2.重复下面过程知道算法收敛{
对于每一个样例(i),计算与它距离最近的质心点,并记下相应中心的编号。
[c^{(i)}:=arg min limits_{j} ||x^{(i)}-u_j||^2
]
对于每一类$j$,重新计算对应的质心
[u_j:=frac{sum limits_{i=1}^{m}1 {c^{(i)}=j }x^{(i)}}{sum limits_{i=1}^{m}1 {c^{(i)}=j}}
]
}
注意:在处理前,先将数据作规范化处理
2. 如何选取起点
与选取随机点相比,随机选取数据点作为质心更加合理。另外,因为K-means算法可能收敛到局部最优点,所以一般采取多次外循环,求得一系列的结果,然后选取结果中(J(c,u))最小的一个。(J(c,u))的定义如下:
[J(c,u)= {1 over m}sum limits _{i=1}^{m}||x^{(i)}-u_{c^{(i)}}||^2
]
3. 如何决定分类个数
关于分类个数的选取,一般是根据需求人工选择的。选择时一般考虑分类的目的是什么,然后根据更好地实现目的进行选择。
其次,有一种可以参考的分类方法,叫做“肘部法则”。如下图所示,一般选取斜率从大到小急剧变化那一点。但有时,也会有斜率一直缓慢变化的情况。

4. 应用
聚类分析可以用于数据压缩。具体思路就是将图片内所有的像素点分成K类,每一类的颜色设置成一个值。下面是例子,将原来的颜色压缩成了16个,仍然可以辨认出图像。

二、主成分分析(PCA)
1.算法步骤
- 1.数据规范化。将数据规范为均值为0,方差为1的数据。
- 2.求解协方差矩阵。
[Sigma {
m{ = }}{1 over {
m{m}}}{X^T}X
]
- 3.对下方差矩阵进行SVD分解。
[[U, S, V] = svd(Sigma)
]
- 4.数据投影。
[Z=XU(:,1:K)
]
- 5.数据恢复
[X_{rec}=ZU(:,1:K)^T
]
2.算法原理
PCA的算法原理是基于SVD分解的一种算法。根据SVD分解中奇异值是从大到小排列,只选取前K项最大值,对原信号进行相应的变换。将相当于N维空间到K维空间的投影。
其中,K值的选取需要满足(frac{sum limits_{i=1}^{K}S_{ii}}{sum limits_{i=1}^{N}S_{ii}} ge 99 \%)。
3.应用举例
- 数据压缩。数据压缩可用来存储数据、加快算法速度。
- 数据可视化。一般设法将数据降到2维或者3维,以便可视化。
下面例子是一个利用PCA算法来提取脸部特征后结果图。这些脸部特征可以用来进行面部识别。
