【ybtoj】【倍增问题】删边问题

题意

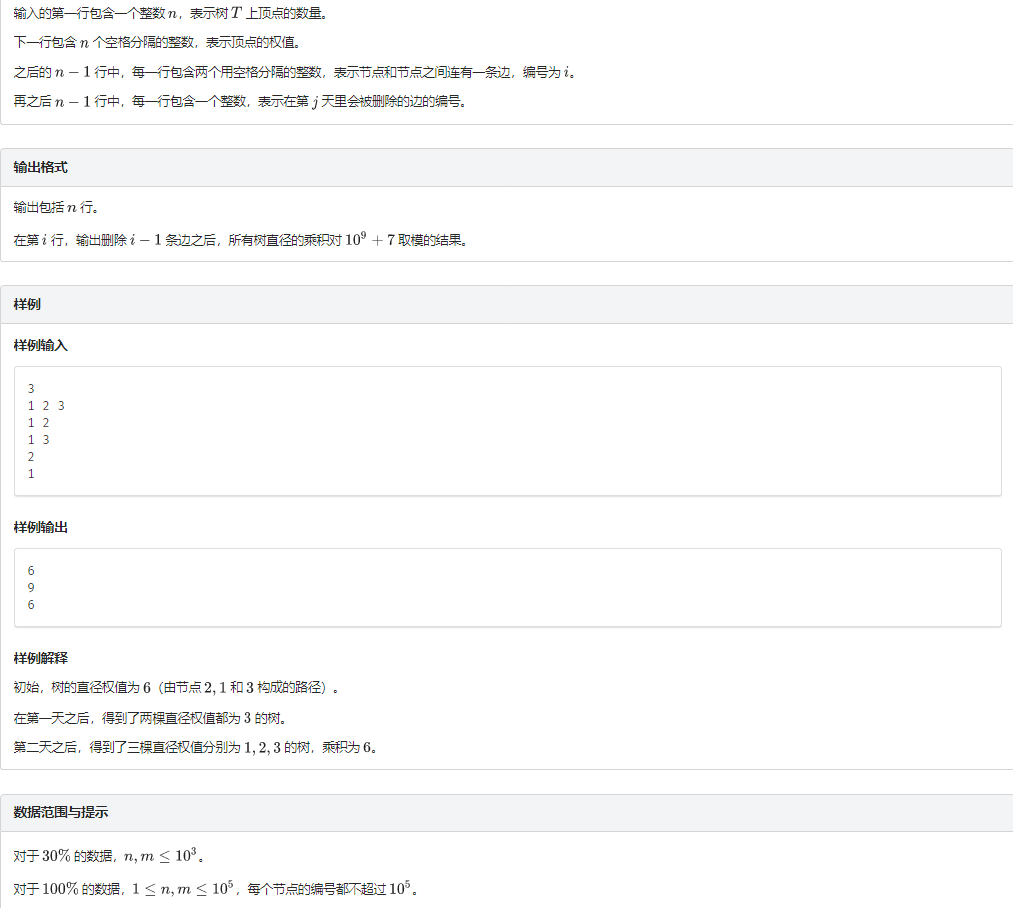
题解

首先想想删除边之后直径的变化，原直径的两个端点也一定是新直径的端点之一
再考虑删除边之后新的直径不好确定，把删边操作改成加边操作，这样新的直径一定在原来两棵树的直径的(4)个端点中选,总共(6)种情况
所以先处理出完整的树的相关信息，比如求(LCA)的(f,dis)数组，用来判断新的直径是选哪两个端点
而且每次合成一棵新的树，相当于除去原来直径再乘上新的直径，由于取模操作，所以要用费马小定理求逆元

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,mod = 1e9+7,N = 1e5+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
int n,del[N],dep[N],f[N][21],fd[N];
int head[N<<1],ecnt=-1; 
ll inv,maxn[2],dis[N],d[N][2],w[N];
ll ans[N];
struct edge
{
	int nxt,to; 
}a[N<<1];
struct E
{
	int x,y;
}id[N];
void add(int x,int y)
{
	a[++ecnt]=(edge){head[x],y};
	head[x]=ecnt;
}

inline void init(){for(int i=1;i<=n;i++) fd[i]=i;}
int find(int x)
{
	if(fd[x]==x) return x;
	return fd[x]=find(fd[x]);
}
void merge(int x,int y){fd[find(x)]=find(y);}
void dfs(int u,int fa)
{
	dep[u]=dep[fa]+1;
	for(int i=1;i<=20;i++) f[u][i]=f[f[u][i-1]][i-1];
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(v==fa) continue;
		f[v][0]=u;
		dis[v]=dis[u]+w[v];
		dfs(v,u);
	}
}
int lca(int x,int y)
{
	if(x==y) return x;
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--)
		if(f[x][i]&&dep[f[x][i]]>=dep[y]) x=f[x][i];
	if(x==y) return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i]) 
			x=f[x][i],y=f[y][i];
	return f[x][0]; 
}
inline ll Dis(int x,int y){return dis[x]+dis[y]-2*dis[lca(x,y)]+w[lca(x,y)];}
ll qpow(ll x,ll y)
{
	ll ret=1;
	while(y)
	{
		if(y&1) ret=ret*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return ret;
}
int main()
{
	memset(head,-1,sizeof(head));
	n=read(),init();
	ans[1]=1;
	for(int i=1;i<=n;i++) w[i]=read(),d[i][1]=d[i][0]=i,ans[1]=ans[1]*w[i]%mod;
	for(int i=1;i<n;i++)
	{
		int u=read(),v=read();
		add(u,v),add(v,u);
		id[i]=(E){u,v};
	}
	for(int i=n;i>=2;i--) del[i]=read();
	dis[1]=w[1];
	dfs(1,0); 
	for(int i=2;i<=n;i++)
	{
		//printf("#%d:
",i);
		ans[i]=ans[i-1];
		int x=find(id[del[i]].x),y=find(id[del[i]].y);
		inv=qpow(Dis(d[x][0],d[x][1])*Dis(d[y][0],d[y][1])%mod,mod-2); 
		//printf("inv=%lld
",inv);
		//printf("d1,d2,d3,d4:%d,%d,%d,%d
",d[x][0],d[x][1],d[y][0],d[y][1]);
		ll D=Dis(d[x][0],d[x][1]);
		maxn[0]=d[x][0],maxn[1]=d[x][1];
		if(D<Dis(d[x][0],d[y][0])) D=Dis(d[x][0],d[y][0]),maxn[0]=d[x][0],maxn[1]=d[y][0];
		if(D<Dis(d[x][0],d[y][1])) D=Dis(d[x][0],d[y][1]),maxn[0]=d[x][0],maxn[1]=d[y][1];
		if(D<Dis(d[x][1],d[y][0])) D=Dis(d[x][1],d[y][0]),maxn[0]=d[x][1],maxn[1]=d[y][0];
		if(D<Dis(d[x][1],d[y][1])) D=Dis(d[x][1],d[y][1]),maxn[0]=d[x][1],maxn[1]=d[y][1];
		if(D<Dis(d[y][0],d[y][1])) D=Dis(d[y][0],d[y][1]),maxn[0]=d[y][0],maxn[1]=d[y][1];
		merge(x,y);
		//printf("maxn:%lld %lld
",maxn[0],maxn[1]);
		d[fd[x]][0]=maxn[0],d[fd[x]][1]=maxn[1];
		ans[i]=ans[i]*inv%mod*D%mod;
		//printf("D=%lld
",D);
	}
	for(int i=n;i>=1;i--)
		printf("%lld
",ans[i]); 
	return 0;
}