【ybtoj】【倍增问题】运输计划

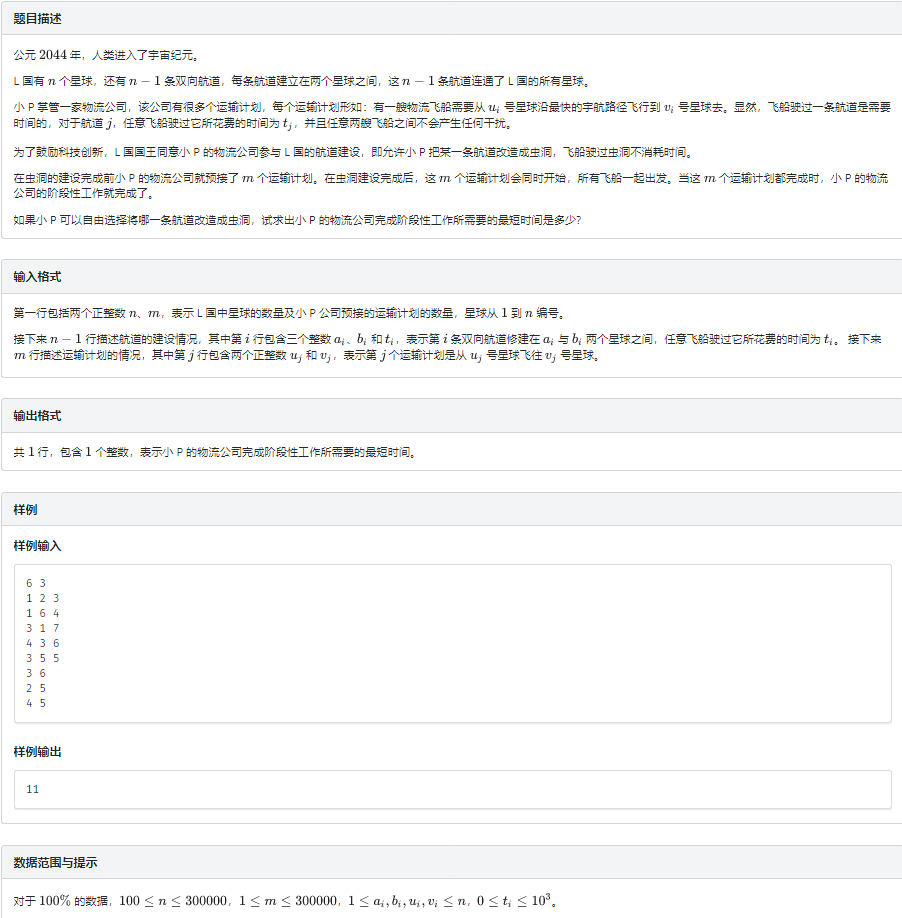
题意

题解

首先可以想到二分答案（二分时间(mid)）
那么对答案有影响的路径就只有花费时间(>mid)的路径
考虑减少一条边，一定是在这些路径的公共部分的花费时间最大的一条边，记为A
如果(最大的路径-w[A]<=mid)，那么说明(mid)可行，否则不可行
如何记录哪些边是公共部分？考虑差分（点差分）
提供两种做法：

• 单纯点差分，(dif[x]++,dif[y]++,dif[lca]--,dif[fa[lca]]--)，最终找到的公共边就是两个端点都被所有路径经过的边
• 边权化点权，(dif[x]++,dif[y]++,dif[lca]-=2)，把每一个点的差分权值的意义设定为它到它的父亲的边被经过的次数，那么最终找到的公共边就是该点到其父亲的边
  对于差分数组求子树前缀和，可以用(dfs)
  也可以用一个循环求解（常数优化）：(for(int i=n;i>=1;i--) dif[fa[rnk[i]]]+=dif[rnk[i]];)其中(rnk)数组存的是(dfn[i])对应的真实节点，倒序枚举就能保证从子树不断向上更新父亲节点（(dfs)序性质）
  代码找人帮忙卡了常，有些地方略丑

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 3e5+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
int head[N<<1],ecnt=-1,dis[N],maxn,val[N];
int dep[N],f[N][21],dfn[N],rnk[N],tim;
int n,m;
struct edge
{
	int nxt,to,w; 
}a[N<<1];
struct E
{
	int x,y,dis, lca;
	inline bool operator < (const E oth)const {return dis>oth.dis;}
}e[N<<1];
int d[N], ff[N];
inline void add(int x,int y,int w)
{
	a[++ecnt]=(edge){head[x],y,w};
	head[x]=ecnt;
}
void dfs(int u,int fa)
{
	dep[u]=dep[fa]+1;
	dfn[u]=++tim,rnk[tim]=u;
	for(int i=1;i<=20;i++) f[u][i]=f[f[u][i-1]][i-1];
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(v==fa) continue;
		val[v]=a[i].w;
		ff[v] = f[v][0]=u;
		dis[v]=dis[u]+a[i].w;
		dfs(v,u);
	}
}
int lca(int x,int y)
{
	if(x==y) return x;
	if(dep[x]<dep[y]) swap(x,y);
	for(int i=20;i>=0;i--)
		if(f[x][i]&&dep[f[x][i]]>=dep[y]) x=f[x][i];
	if(x==y) return x;
	for(int i=20;i>=0;i--)
		if(f[x][i]!=f[y][i]) 
			x=f[x][i],y=f[y][i];
	return f[x][0]; 
}
inline int Dis(int x,int y, int lca){return dis[x]+dis[y]-(dis[lca]<<1);}
void dcf(int u,int fa)
{
	val[u]=d[u];
	for(int i=head[u];~i;i=a[i].nxt)
	{
		int v=a[i].to;
		if(v==fa) continue;
		dcf(v,u);
		val[u]+=val[v];
	}
}
bool check(int mid)
{
	//memset(val,0,sizeof(val));
	memset(d,0,(n + 1) * sizeof(int)); 
	int cnt=0;
	for(E *ei= e + 1;ei<=e + m;ei++)
	{
		if(ei->dis<=mid) break;
		cnt++;
		d[ei->x]++,d[ei->y]++,d[ei->lca]-=2;
	}
	//dcf(1,0);
	for(int *i=rnk + n;i != rnk;i--) 
		d[ff[i[0]]]+=d[i[0]];
	int maxn=0;
	for(int i=1;i<=n;i++)
		if(d[i]==cnt)
		{
			maxn=maxn>val[i]?maxn:val[i];
		}
	//printf("dis=%d,maxn=%d,mid=%d
",e[1].dis,maxn,mid);
	return e[1].dis-maxn<=mid;
}

int main()
{
	memset(head,-1,sizeof(head));
	n=read(),m=read();

	for(int i=1;i<n;i++) 
	{
		int u=read(),v=read(),w=read();
		add(u,v,w),add(v,u,w);
	}	
	dfs(1,0);
	for(int i=1;i<=m;i++)
	{
		e[i].x=read(),e[i].y=read();
		e[i].lca = lca(e[i].x, e[i].y);
		e[i].dis=Dis(e[i].x,e[i].y, e[i].lca);
		maxn=max(maxn,e[i].dis);
	}
	sort(e+1,e+m+1);
	int l=0,r=maxn;
	while(l<r)
	{
		int mid=(l+r)>>1;
		if(check(mid)) r=mid;
		else l=mid+1;
	}
	printf("%d",l);
	return 0;
}