【ybtoj】【RMQ问题】与众不同

题意

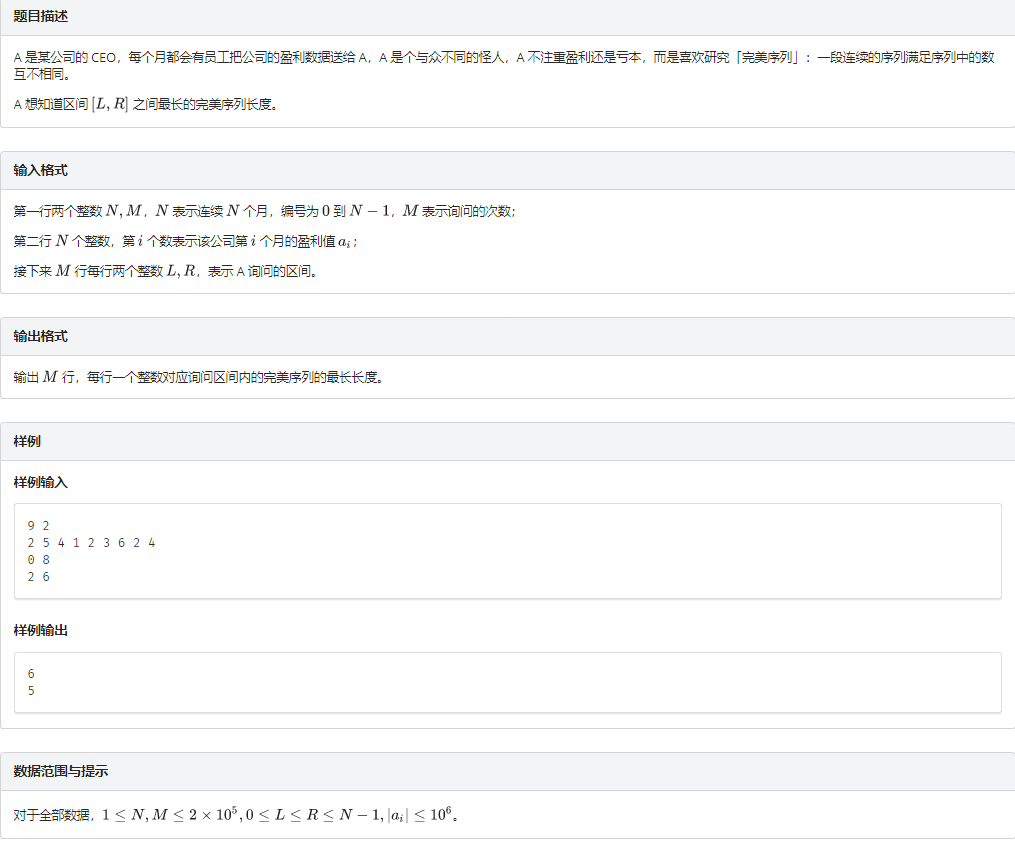
题解

虽然在(RMQ)的章节里，但是这题的重点不在(RMQ)，只是一个优化
考虑如何找到一段完美序列
记录(lst[val])表示val值上次出现的位置,(pre[i])表示以(i)为结尾的完美序列的起点
那么转移式很显然，(pre[i]=max(lst[a[i]]+1,pre[i-1]))
对于一段询问的区间，考虑如何求完美序列的长度
对于区间内每一个点(i),(pre[i])可能在区间外((l)左边),也可能在区间内((l)右边）

• 如果(pre[i]<l),那么以(i)结尾的完美序列长度就是(i-l+1)
• 如果(pre[i]>=l),那么以(i)为结尾的完美序列长度就是(i-pre[i]+1)
  因此可以二分找到一个分界点(now),(now)左边的完美序列最大值为(now-l+1),右边的则为区间内(i-pre[i]+1),记为(f[i]),可以用ST表维护静态区间最大值
  二分的时候注意特判边界情况！

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 2e6+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
map<int,int> lst;
int n,m,a[N],dp[N][22],Log[N],pre[N],f[N];
void buildst()
{
	for(int j=1;(1<<j)<=n;j++)
		for(int i=1;i+(1<<j)-1<=n;i++)
			dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
	int k=0;
	for(int i=1;i<=n;i++)	
	{
		if((1<<k)<=i) k++;
		Log[i]=k-1;
	}
}
inline int query(int l,int r)
{
	int k=Log[r-l+1];
	return max(dp[l][k],dp[r-(1<<k)+1][k]);
}
inline int find(int l,int r)
{
	int L=l;
	while(l<r)
	{
	//printf("find(%d,%d)
",l,r);
		int mid=(l+r)>>1;
		if(pre[mid]<L) l=mid+1;
		else r=mid;
	}
	return l;
}
int main()
{
	n=read(),m=read();
	for(int i=1;i<=n;i++) 
	{
		a[i]=read();
		pre[i]=max(pre[i-1],lst[a[i]]+1); 
		lst[a[i]]=i;
		f[i]=i-pre[i]+1;
		dp[i][0]=f[i];
		//printf("pre[%d]=%d
",i,pre[i]);
	}
	//for(int i = 1 ; i <= n ; i ++)	printf("pre[%d]=%d , f = %d
",i,pre[i],f[i]);
	buildst();
	
	for(int i=1;i<=m;i++)
	{
		int l=read(),r=read();
		l++,r++;
		int now=find(l,r);	
		int ans=(now-1)-l+(1);
		if(pre[r]<=l) {printf("%d
",r-l+1);continue;}
		//printf("now=%d,ans = %d
",now,ans);
		if(now<=r) 
			if(pre[now]>=l)ans=max(ans,query(now,r));
		//printf(" query (%d,%d) = %d
",now,r,query(now,r));
		printf("%d
",ans);
	}
	/*
	while(m--)
	{
		int l = read()+1 , r = read()+1;
		int now = lower_bound(pre+l+1,pre+r+1,l)-pre-1;
		int ans = now - l + 1;
		if(now < r) ans = max(ans,query(now+1,r));
//		printf("(%d,%d)
",l,r);
//		printf("now = %d
",now); 
		printf("%d
",ans);
	}
	*/ 
	return 0;
}
/*
12 3
2 5 4 1 2 3 6 2 4 3 1 0
0 8
2 6
5 11
*/