【ybtoj】【期望问题】期望得分

题意

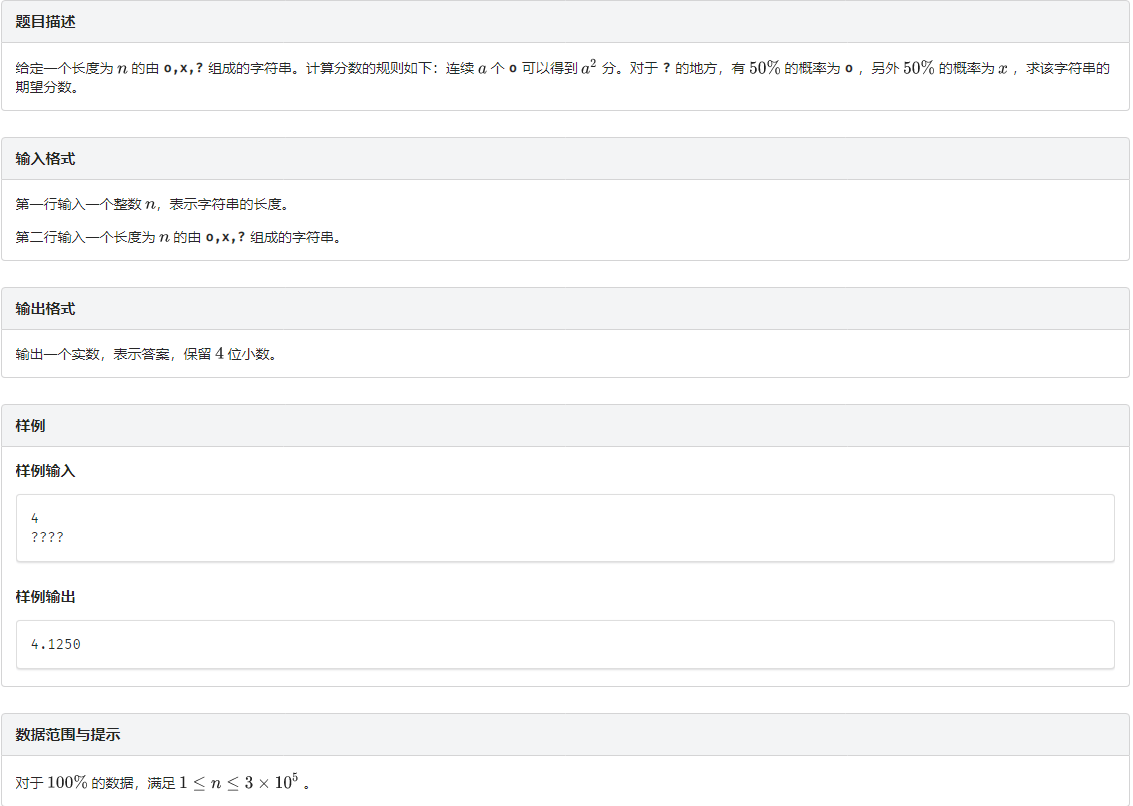
题解

刚接触期望问题，很容易想到 (f(i,j)) 表示前 (i) 个字符，最后有 (j) 个连续的 o 的期望得分。
不过这样还要记录 (p_j) 表示当前末尾出现连续 (j) 个字符的概率，且 (f) 为两维显然空间不足。
所以要充分利用期望的性质：可加性，可乘性。
重新考虑的时候想到连续 (x) 个 o 之后再加上一个 o ，对答案的贡献为 ((x+1)^2-x^2=2x+1).
把 (p) 数组舍去，直接记录当前末尾 o 的期望长度，就可以直接转移。
代码非常简短。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,N = 3e5+10;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
int n;
char s[N];
double elen,ans; 
int main()
{
	n=read();
	scanf("%s",s+1);
	for(int i=1;i<=n;i++) 
	{
		if(s[i]=='o') ans+=2*elen+1,elen++;
		else if(s[i]=='x') elen=0;
		else ans+=(2*elen+1)*0.5,elen=0.5*(elen+1); 
	}
	printf("%.4lf",ans);
	return 0;
}