【ybtoj】【矩阵快速幂】公式推导

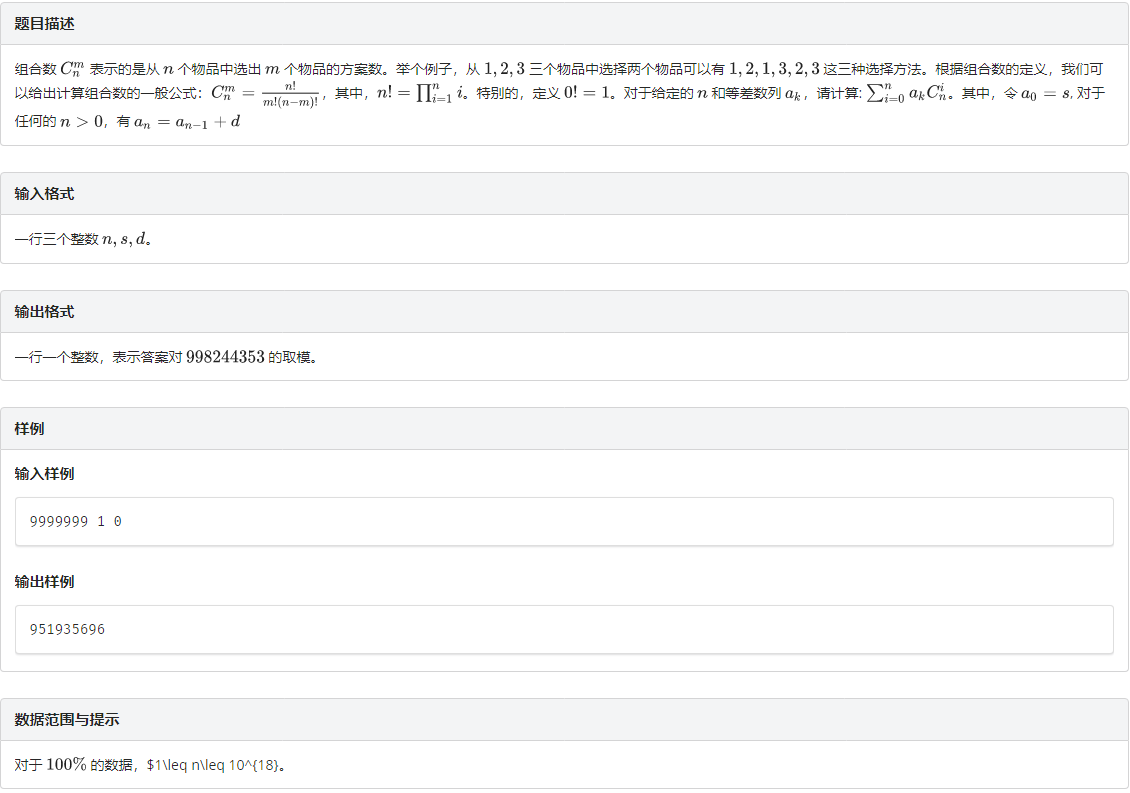
题意

题解

被思维定式坑了...
一开始想的都是怎么用矩阵转移。

• 等差数列很好转移，矩阵里一个 (1) 一个 (d) 即可。
• 组合数不好转移，只能想到 (C_n^m=C_n^{m-1} imes frac{n-m+1}{m}) ，然而由于 (m) 是不断变化的，而且矩阵不好维护除法的形式，思考无果。
  实际上是快速幂的纯数学推导...
  由于 (C_n^k=C_n^{n-k}) ，且这两项的 (a) 值和正好是 (2s+nd) ，所以可以把 (a) 对应的系数提出来，变成(frac{1}{2}(2s+nd) sum limits_{i=0}^n C_n^i) ，根据二项式定理可得(sum limits_{i=0}^n C_n^i=2^n) ，那么原式就变成了((2s+nd) imes 2^n) ，直接快速幂求出即可。

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int INF = 0x3f3f3f3f,mod = 998244353;
inline ll read()
{
	ll ret=0;char ch=' ',c=getchar();
	while(!(c>='0'&&c<='9')) ch=c,c=getchar();
	while(c>='0'&&c<='9') ret=(ret<<1)+(ret<<3)+c-'0',c=getchar();
	return ch=='-'?-ret:ret;
}
ll qpow(ll x,ll y)
{
	ll ret=1;
	while(y)
	{
		if(y&1) ret=ret*x%mod;
		x=x*x%mod;
		y>>=1;
	}
	return ret;
}
ll n,s,d;
int main()
{
	n=read(),s=read(),d=read();
	d%=mod,s%=mod;
	ll ans=((s<<1)+n%mod*d%mod)%mod;
	ans=(ans*qpow(2,n-1))%mod;
	printf("%lld",ans);
	return 0;
}