有向图

1. 什么是有向图

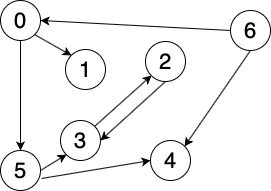
如图中所示，有向图和无向图最大的区别在于每条路径都带有方向性。假如把无向图看成是双行道，可以任意穿梭的话，有向图就是一座只有单行道的城市，而且这些单行道是杂乱无章的。因此要求解一处到另一处的路径问题就会变得复杂起来。

2. 有向图的数据结构

public class Digraph
{
    private final int V; //图的顶点数
    private int E;       //图的边数
    private Bag<Integer>[] adj; //邻接矩阵

    public Digraph(int V)   //图的构造函数
    {
        this.V = V;
        this.E = 0;
        adj = (Bag<Integer>[]) new Bag[V];
        for(int v=0;v<V;v++)
            adj[v] = new Bag<Integer>();
    }

    public int V() { return V; }
    public int E() {return E; }
    
    public void addEdge(int v, int w) //增加边
    {
        adj[v].add(w);
        E++;
    }

    public Digraph reverse(Digraph G) //形成反向图，这个之后会有很大用处
    {
        Digraph R = new Digraph(V);
        for(int v=0;v<V;v++)
            for(int w: adj(v))
                R.addEdge(w, v);
    }

    public Iterable<Integer> adj(int v)
    {
        return adj[v];
    }
}

以上为图的数据结构，之后会频繁用到。

3.有向图的可达性

可达性主要是为了解决三个问题：

1）给定一副有向图和一个出发点，可以到达哪些点？

2）给定一副有向图和很多出发点，总共可以到达哪些点？

3）给定一副有向图、一个出发点s和另一个顶点v，s和v之间是否存在一条有向路径？

这三个问题其实都可以通过深度优先搜索来解决。

public class DirectedDFS
{
    private boolean[] marked;
    private DirectDFS(Digraph G, int s)
    {
        marked = new boolean[G.V()];
        dfs(G, s);
    }

    private DirectedDFS(Digraph G, Iterable<Integer> sources)
    {
        marked = new boolean[G.V()];
        for(int s: sources)
            dfs(G, s);
    }

    private void dfs(Digraph G, int v) //深度优先搜索
    {
        marked[v] = true;
        for(int w: G.adj[v])
            if(!marked[w])
                dfs(G, w);
    }

    public boolean marked(int v)
    {
        return marked[v];
    }
}

 多点可达性的一个很重要的应用就是在内存管理系统。在一副有向图中，一个顶点表示一个对象，一条边则表示一个对象对另一个对象的引用。不能通过引用被访问到的对象则应该被系统回收。

4.有向图中的环

虽然有向图中环的数量和大小也是有用的信息，但是在实际应用过程中，我们更多的只关心存不存在有向环。

public class DirectedCycle
{
    private boolean[] marked; //记录顶点是否被遍历过
    private boolean[] onStack; //记录下处在当前的递归循环中的所有顶点
    private int[] edgeTo;
    private Stack<Integer> cycle; //存所有在换上的顶点，注意只存一个

    public DirectedCycle(Digraph G) {
        marked = new boolean[G.V()];
        onStack = new boolean[G.V()];
        edgeTo = new int[G.V()];
        for(int v;v<G.V(); v++)
        {
            if(!marked[v])
                dfs(G, v);
        }
    }

    public void dfs(Digraph G, int v) //深度优先算法
    {
       marked[v] = true;
       onStack[v] = true;
       for(int w:G.adj(v))
       {
           if(this.hasCycle()) return;
           else if(!marked[w]) 
           {
               edgeTo[w] = v;
               dfs(G, w);
           }
           else if(onStack[w])
           {
               cycle = new Stack<Integer>();
               for(int x = v;x!=w;x = edgeTo[x])
                   cycle.push(x);
               cycle.push(w);
               cycle.push(v);
           }
       }
       onStack[v] = false; //递归结束则置为false
    }

    public boolean hasCycle() //记录是否存在环
    {
        return cycle!=null;
    }
}

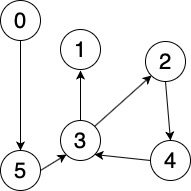
在以上的代码中，需要注意onStack数组只记录在当前递归循环中的顶点，也就是说假如顶点v在当前路径中，那么onStack[v] = true，否则为false。当递归循环一层层结束，那么原来置为true的顶点，又一层层被置为false。以下图为例，在0 - 5 - 3 - 1 这条递归路径中，onStack[0], onStack[5], onStack[3], onStack[1]被依次置为true。随后onstack[1]因为走到尽头而退出，onStack[1] = false, 随后onStack[2], onStack[4]又被置为true，当4之后又到3时，发现3已经在当前路径中（onStack[3] = true)，从而找到了环。而整个环的路径都可以由edgeTo这个数组找到。

5. 有向图的拓扑排序

当确定有向图中不存在环以后，就可以得到该有向图的拓扑排序。所谓拓扑排序，就是按照箭头所指的方向进行排序，例如0->5路径，意味着在拓扑排序中，先有0，再有5。

值得注意的是，有向图的排序可能比想象中要容易很多，只需要在深度优先算法中加入一行代码就可以完成排序。这一方法中潜在的思想在于：深度优先搜索正好只会访问每个节点一次。

在典型的应用中，存在三种比较重要的排序方法。

1）前序：在递归调用之前加入排序队列。

2）后序：在递归调用完成以后加入排序队列。

3）逆后序：在递归调用完成以后将顶点压入栈。

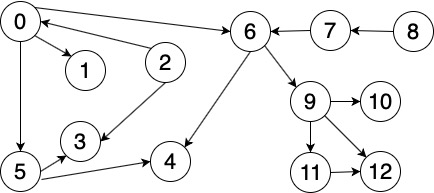
 以上图为例。

前序为 0 - 5 - 4 - 1 - 6 - 9 - 11 - 12 - 10 - 2 - 3 - 7- 8。前序就是dfs的调用顺序。

后序为 4 - 3 - 1 - 12 - 11 - 10 - 9 - 6 - 0 - 3 - 2 - 7 - 8。后序就是顶点遍历完成的顺序。

逆后序为 8 - 7 - 2 - 3 - 0 - 6 - 9 - 10 - 11 - 12 - 1 - 3 - 4。逆后序就是后序的逆。

public class DepthFirstOrder
{
    private boolean[] marked;
    private Queue<Integer> pre; //前序
    private Queue<Integer> post; //后序
    private Stack<Integer> reversePost; //逆后序

    public DepthFirstOrder(Digraph G)
    {
        marked = new boolean[G.V()];
        pre = new Queue<Integer>();
        post = new Queue<Integer>();
        reversePost = new Stack<Integer>();
        for(int v = 0; v<G.V(); v++)
        {
            if(!marked[v])
                dfs(G, v);
        }
    }

    public void dfs(Digraph G, int v)
    {
        marked[v] = true;
        pre.enqueue(v);

        for(int w : G.adj(v))
        {
            if(!marked[w])
                dfs(G, w);
        }
        post.enqueue(v);
        reversePost.push(v);
    }

    public Queue<Integer> pre()
    { return pre; }

    public Queue<Integer> post()
    { return post;}

    public Stack<Integer> reversePost()
    { return reversePost;}
    
}

一个重要的结论为，一副有向无环图的拓扑排序即为所有顶点的逆后序排列。

以课程安排的应用为例。x -> y意味着，y课程比较难，必须要先学x才能学y。于是前序排列，就成了部分按照从易到难的顺序的排列，剩余部分随机排列的顺序。而后序则是严格满足最深路径排在最前，最后也就是从难到易的排列。于是逆排序就是严格从易到难的排列。

6. 有向图的强连通性 - Kosaraju算法

由于有向图具有单行道的特点，因此区分了强连通性和弱连通性的概念。加入只是单向连接，例如存在有向路径从A到B，而不存在有向路径从B到A，则为弱连通性。加入同时存在从A到B和从B到A的有向路径，则成A和B有强连通性。

强连通分量指的是所有相互具有强连通的顶点的最大子集。Kosaraju算法很好得解决了求解强连通分量的问题。虽然易于实现，但是确实又些难以理解。在此也感谢nullzx的解释。核心在于，假设A和B分别为两个强连通分量，A能到B，而B到不了A的情况下，只有先搜索B，再搜索A，才能在一次搜索中正确识别两个连通分量。假如先搜索A，那么A直接能连通到B，那么一次搜索就无法知道到底有几个连通分量。因此顺序非常重要。

总结来说Kosaraju分为三步实现：

1）构造反向图G^R

2）对G^R进行深度优先搜索，并得到逆后序排序

3）按照2）中得到的顺序，对G进行标准的深度优先搜索。

其实Kosaraju的证明也不是很难，看懂之后会发现并不复杂，现给出简单的解释。

为了证明s和v为强连通分量，那么需要满足：

条件一：存在s到v的有向路径

条件二：存在v到s的有向路径

假如在3）的搜索中，先执行dfs(G, s)，再执行dfs(G, v)，并且发现存在s到v的路径，那么条件一满足。既然3）的搜索中，先有s，再有v，这说明在2）的搜索过程中，v先完成搜索，s后完成。那么就可能存在两种情况，一种是先调用dfs(G^R,v)，另一种是先调用dfs(G^R, s)。既然G中存在s到v的路径，那么G^R中肯定存在v到s的路径，因此假如先调用v的话，那么s肯定比v先结束，这与之前的结论相反，因此不可能。所以只能是第二种，而第二种也意味着存在s到v的路径，也就是G中v到s的路径，因此条件二也满足。

参考资料：《算法》第四版