时间序列预测——Tensorflow.Keras.LSTM

1、测试数据下载

https://datamarket.com/data/set/22w6/portland-oregon-average-monthly-bus-ridership-100-january-1973-through-june-1982-n114#!ds=22w6&display=line

2、LSTM预测

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import datetime
from dateutil.relativedelta import relativedelta

df = pd.read_csv("C:\Users\Administrator\Downloads\portland-oregon-average-monthly-.csv", 
index_col=0)

df.index.name=None #将index的name取消
df.reset_index(inplace=True)
df.drop(df.index[114], inplace=True)
start = datetime.datetime.strptime("1973-01-01", "%Y-%m-%d") #把一个时间字符串解析为时间元组
date_list = [start + relativedelta(months=x) for x in range(0,114)] #从1973-01-01开始逐月增加组成list
df['index'] =date_list
df.set_index(['index'], inplace=True)
df.index.name=None
df.columns= ['riders']
df['riders'] = df.riders.apply(lambda x: int(x)*100)
df.riders.plot(figsize=(12,8), title= 'Monthly Ridership', fontsize=14)
plt.show()

data = df.iloc[:,0].tolist()

def data_processing(raw_data, scale=True):
    if scale == True:
        return (raw_data-np.mean(raw_data))/np.std(raw_data)#标准化
    else:
        return (raw_data-np.min(raw_data))/(np.max(raw_data)-np.min(raw_data))#极差规格化
TIMESTEPS = 12

'''样本数据生成函数'''
def generate_data(seq):
    X = []#初始化输入序列X
    Y= []#初始化输出序列Y
    '''生成连贯的时间序列类型样本集，每一个X内的一行对应指定步长的输入序列，Y内的每一行对应比X滞后一期的目标数值'''
    for i in range(len(seq) - TIMESTEPS - 1):
        X.append([seq[i:i + TIMESTEPS]])#从输入序列第一期出发，等步长连续不间断采样
        Y.append([seq[i + TIMESTEPS]])#对应每个X序列的滞后一期序列值
    return np.array(X, dtype=np.float32), np.array(Y, dtype=np.float32)


'''对原数据进行尺度缩放'''
data = data_processing(data)

'''将所有样本来作为训练样本'''
train_X, train_y = generate_data(data)

'''将所有样本作为测试样本'''
test_X, test_y = generate_data(data)


from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
from tensorflow.keras.layers import LSTM

model = Sequential()
model.add(LSTM(16, input_shape=(train_X.shape[1], train_X.shape[2])))
model.add(Dense(train_y.shape[1]))
model.compile(loss='mse', optimizer='adam', metrics=['accuracy'])
model.fit(train_X, train_y, epochs=1000, batch_size=len(train_X), verbose=2, shuffle=False)

#scores = model.evaluate(train_X, train_y, verbose=0)
#print("Model Accuracy: %.2f%%" % (scores[1] * 100))

result = model.predict(train_X, verbose=0)

'''自定义反标准化函数'''
def scale_inv(raw_data,scale=True):
    data1 = df.iloc[:, 0].tolist()
    if scale == True:
        return raw_data*np.std(data1)+np.mean(data1)
    else:
        return raw_data*(np.max(data1)-np.min(data1))+np.min(data1)

'''绘制反标准化之前的真实值与预测值对比图'''
plt.figure()
plt.plot(scale_inv(result), label='predict data')
plt.plot(scale_inv(test_y), label='true data')
plt.title('none-normalized')
plt.legend()
plt.show()


def generate_predata(seq):
    X = []#初始化输入序列X
    X.append(seq)
    return np.array(X, dtype=np.float32)

datalist = data.tolist()
pre_result = []
for i in range(50):
    pre_x = generate_predata(datalist[len(datalist) - TIMESTEPS:])
    #pre_x = pre_x[np.newaxis,:,:]
    pre_x = np.reshape(pre_x, (1, 1, TIMESTEPS))
    pre_y = model.predict(pre_x)
    pre_result.append(pre_y.tolist()[0])
    datalist.append(pre_y.tolist()[0][0])
all = result.tolist()
all.extend(pre_result)
'''绘制反标准化之前的真实值与预测值对比图'''
plt.figure()
plt.plot(scale_inv(np.array(all)), label='predict data')
plt.plot(scale_inv(test_y), label='true data')
plt.title('none-normalized')
plt.legend()
plt.show()

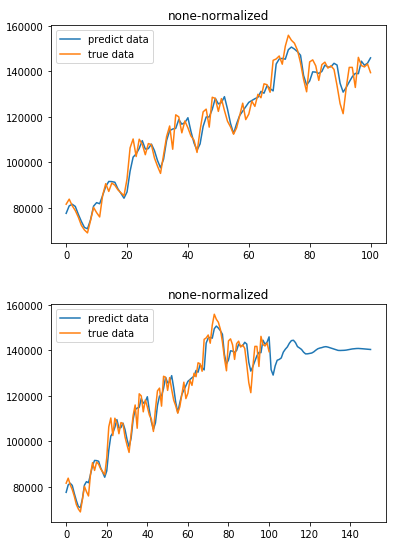
3、运行效果