问题引入
max f(x, y)
s.t.
g(x,y) <= 0
几何解释
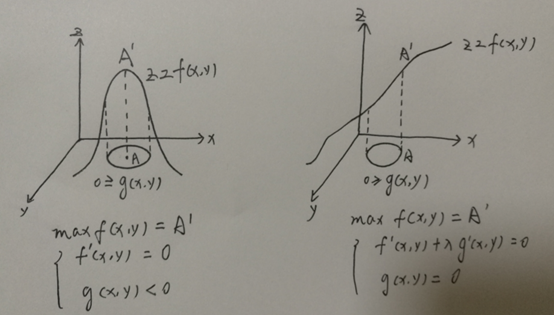
a. g(x ,y) <= 0为上图中z = 0平面中的圆,圆的边表示g(x, y) = 0,圆的内部表示g(x, y) < 0。
b. z = f(x, y)为上图中的曲面。
上述极值问题就是要求当点(x, y)落在圆内时(包括圆的边),f(x, y)的最大值。
1、 如果极值点在圆内,则显然有
f'(x, y) = 0
g(x, y) < 0
2、 如果极值点在圆边上,有拉格朗日乘子法我们知道
f’(x, y) + λg’(x ,y) = 0
g(x, y) = 0
如果是数学考试,我们直接求出上面两种情况的所有解(x, y),再带入f(x, y)计算,选取最大值即可。
对偶问题
稍微修改一下文章开头的极值问题,得到新的极值问题1
min f(x, y)
s.t.
g(x,y) <= 0
拉格朗日函数如下
F(x, y, λ) = f(x, y) + λg(x, y)
我们对x, y求导数并令其为0,即
F’(x, y, λ) = f’(x, y) + λg’(x, y) = 0
场景1等价于
F’(x, y, λ) = 0
g(x, y) < 0
λ = 0
场景2等价于
F’(x, y, λ) = 0
g(x, y) = 0
λ > 0
场景二极小值点在圆边上,如果此时f(x, y)与g(x, y)梯度方向相同,说明点(x ,y)往圆内移动,f(x, y)的值会和g(x, y)的值一样减小,显然此时圆边上的点(x, y)不是极小值点。所以如果f(x, y)的极小值点在圆边上,必然f(x, y)与g(x, y)梯度方向相反,即λ > 0。
综合上述两种情况,极值问题1的对偶问题2如下(对偶问题解决了,原问题也就解决了)
max F(x, y, λ) = f(x, y) + λg(x, y)
s.t.
g(x, y) <= 0
λ >= 0
λg(x, y) = 0
点(x, y)在圆圈g(x, y) <= 0内,对于λ >= 0,我们有F(x, y, λ) <= f(x, y),于是F(x, y, λ)的上界就是f(x, y)的下界。
我们把
g(X) <= 0
λ >= 0
λg(X) = 0
称作KKT条件。X表示向量(x1; x2; …; xn)。