局部异常因子算法-Local Outlier Factor(LOF)
在数据挖掘方面,经常需要在做特征工程和模型训练之前对数据进行清洗,剔除无效数据和异常数据。异常检测也是数据挖掘的一个方向,用于反作弊、伪基站、金融诈骗等领域。
异常检测方法,针对不同的数据形式,有不同的实现方法。常用的有基于分布的方法,在上、下α分位点之外的值认为是异常值(例如图1),对于属性值常用此类方法。基于距离的方法,适用于二维或高维坐标体系内异常点的判别,例如二维平面坐标或经纬度空间坐标下异常点识别,可用此类方法。 
这次要介绍一下一种基于密度的异常检测算法,局部异常因子LOF算法(Local Outlier Factor)
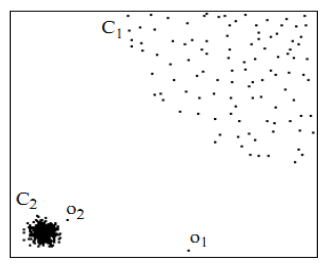
用视觉直观的感受一下,如图2,对于C1集合的点,整体间距,密度,分散情况较为均匀一致,可以认为是同一簇;对于C2集合的点,同样可认为是一簇。o1、o2点相对孤立,可以认为是异常点或离散点。现在的问题是,如何实现算法的通用性,可以满足C1和C2这种密度分散情况迥异的集合的异常点识别。LOF可以实现我们的目标。
下面介绍LOF算法的相关定义:
1) d(p,o):两点p和o之间的距离。
2) k-distance:第k距离
对于点p的第k距离dk(p)定义如下:
dk(p)=d(p,o),并且满足:
a) 在集合中至少有不包括p在内的k个点o' ∈ C{x ≠ p}, 满足d(p,o') ≤ d(p,o) 。
b) 在集合中最多有不包括p在内的k−1个点o' ∈ C{x ≠ p},满足d(p,o') < d(p,o)。
如下图,离p第5远的点在以p为圆心,d5(p)为半径的
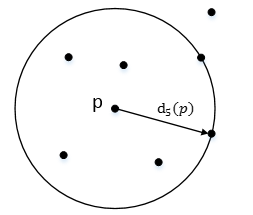
点p的第k距离邻域Nk(p),就是p的第k距离即以内的所有点,包括第k距离。
因此p的第k邻域点的个数 |Nk(p)| ≥ k。
4) reach-distance:可达距离
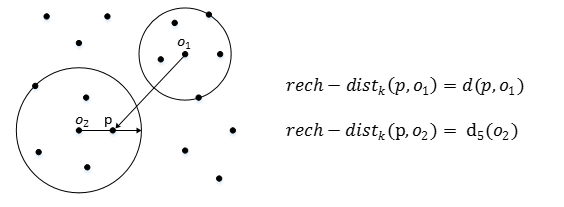
点o到点p的第k可达距离定义为:reach−distancek(p,o) = max{dk(o), d(p,o)}
也就是,点o到点p的第k可达距离,至少是o的第k距离,或者为o、p间的真实距离。
5) local reachability density:局部可达密度
点p的局部可达密度表示为: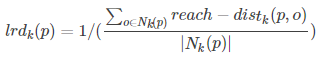 表示点p的第k邻域内的点到p的平均可达距离的倒数。
表示点p的第k邻域内的点到p的平均可达距离的倒数。
6) local outlier factor:局部离群因子
点p的局部离群因子表示为:
表示点p的邻域点Nk(p)的局部可达密度与点p的局部可达密度之比的平均数。
local outlier factor越接近1,说明p的其邻域点密度差不多,p可能和邻域同属一簇;
local outlier factor越小于1,说明p的密度高于其邻域点密度,p为密集点;
local outlier factor越大于1,说明p的密度小于其邻域点密度,p越可能是异常点。
因为LOF对密度的是通过点的第k邻域来计算,而不是全局计算,因此得名为“局部”异常因子,这样,对于图1的两种数据集C1和C2,LOF完全可以正确处理,而不会因为数据密度分散情况不同而错误的将正常点判定为异常点。
转自:https://blog.csdn.net/wangyibo0201/article/details/51705966