数据模型
规则:
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
插入过程:
若二叉排序树为空,则待插入结点S作为根结点插入到空树中;
当非空时,将待插结点关键字S->key和树根关键字t->key进行比较,若s->key = t->key,则无须插入,
若s->key < t->key,则插入到根的左子树中,若s->key > t->key,则插入到根的右子树中。
而子树中的插入过程和在树中的插入过程相同,如此进行下去,直到把结点s作为一个新的树叶插入到二叉排序树中,
或者直到发现树已有相同关键字的结点为止。
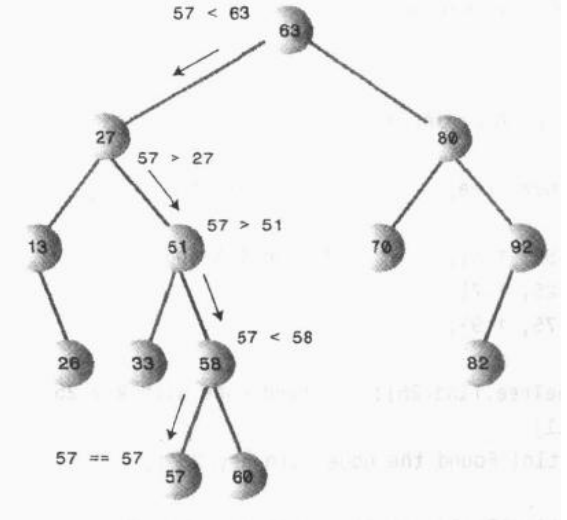
查找过程:
假定二叉排序树的根结点指针为 root ,给定的关键字值为 K ,则查找算法可描述为:
① 置初值: q = root ;
② 如果 K = q -> key ,则查找成功,算法结束;
③ 否则,如果 K < q -> key ,而且 q 的左子树非空,则将 q 的左子树根送 q ,转步骤②;否则,查找失败,结束算法;
④ 否则,如果 K > q -> key ,而且 q 的右子树非空,则将 q 的右子树根送 q ,转步骤②;否则,查找失败,算法结束。
删除过程:
删除节点分为几种情况:
1.删除的节点为叶子节点:直接删除。
2.删除的节点只存在左子树或右子树:删除节点的父节点直接指向子树节点。
3.删除的节点同时存在左子树和右子树:将删除节点的左子树的最右节点或右子树的最左节点替换删除节点,同时删除替换节点,再将删除节点指向子树节点。
节点类
class Node { int key; int value; Node leftChild; Node rightChild; public Node(int key, int value) { this.key = key; this.value = value; this.leftChild = null; this.rightChild = null; } public Node(int key, int value, Node leftChild, Node rightChild) { super(); this.key = key; this.value = value; this.leftChild = leftChild; this.rightChild = rightChild; } public Node() { } @Override public String toString() { return "Node [key=" + this.key + ", value=" + this.value + ", leftChild=" + this.leftChild + ", rightChild=" + this.rightChild + "]"; } public int getKey() { return this.key; } public void setKey(int key) { this.key = key; } public int getValue() { return this.value; } public void setValue(int value) { this.value = value; } public Node getLeftChild() { return this.leftChild; } public void setLeftChild(Node leftChild) { this.leftChild = leftChild; } public Node getRightChild() { return this.rightChild; } public void setRightChild(Node rightChild) { this.rightChild = rightChild; } }
操作实现
public class BinaryTree extends AbsBinaryTree { private Node root; public Node getRoot() { return this.root; } public void setRoot(Node root) { this.root = root; } // 二叉排序树查找节点 // 找到和key相等则返回相应节点,否则返回 null。 @Override public Node find(int key) { // TODO Auto-generated method stub Node currentNode = this.root; // currentNode.key和 key不等才需要循环 while ((currentNode != null) && (currentNode.key != key)) { if (key < currentNode.key) { currentNode = currentNode.leftChild; } else if (key > currentNode.key) { currentNode = currentNode.rightChild; } } return currentNode; }
@Override public void insert(int key, int value) { if (this.root == null) { this.root = new Node(key, value); return; } Node currentNode = this.root; Node parentNode = this.root;// 指向currentNode节点的父节点 boolean isLeftChild = true; // 寻找插入位置 while (currentNode != null) { parentNode = currentNode; if (key < currentNode.key) { currentNode = currentNode.leftChild; isLeftChild = true; } else if (key > currentNode.key) { currentNode = currentNode.rightChild; isLeftChild = false; } else { // 插入的节点key和二叉树中节点key相等无需插入 // parentNode 和 currentNode两个引用指向相同Node对象,引用变量相等,只需要更改value break; } } // 插入节点 if (parentNode != currentNode) { Node newNode = new Node(key, value); if (isLeftChild) { parentNode.leftChild = newNode; } else { parentNode.rightChild = newNode; } } else { // 如果待插入节点和二叉树中节点一样;则只要更改值 currentNode.setValue(value); } } @Override public boolean delete(int key) { // TODO Auto-generated method stub Node currentNode = this.root;// 用来保存待删除节点 Node parentNode = this.root;// 用来保存待删除节点的父亲节点 boolean isLeftChild = true;// 用来保存待删除节点是父亲节点的左孩子还是右孩子 // 寻找删除节点并记录删除节点的父节点以及他是父节点的左孩子还是右孩子 while ((currentNode != null) && (currentNode.key != key)) { parentNode = currentNode; if (key < currentNode.key) { currentNode = currentNode.leftChild; isLeftChild = true; } else { currentNode = currentNode.rightChild; isLeftChild = false; } } if (currentNode == null) return false;// 空树 // 要删除的节点为叶子节点,删除的第一种情况 if ((currentNode.leftChild == null) && (currentNode.rightChild == null)) { if (currentNode == this.root) { this.root = null; } else if (isLeftChild) { parentNode.leftChild = null; } else { parentNode.rightChild = null; } // 要删除的节点只有左孩子 第二种情况 } else if ((currentNode.rightChild == null) && (currentNode.leftChild != null)) { if (currentNode == this.root) { this.root = currentNode.leftChild; } else if (isLeftChild) { parentNode.leftChild = currentNode.leftChild; } else { parentNode.rightChild = currentNode.leftChild; } // 要删除的节点只有右孩子 第三种情况 } else if ((currentNode.leftChild == null) && (currentNode.rightChild != null)) { if (currentNode == this.root) { this.root = currentNode.rightChild; } else if (isLeftChild) { parentNode.leftChild = currentNode.rightChild; } else { parentNode.rightChild = currentNode.rightChild; } } // 最后一种情况,待删除节点既有左子树又有右子树 else { // 将待删除节点的右子树最小节点赋值给删除节点的key,value,那么删除后新的二叉树也是二叉排序树 // 思路:删除右子树中key值最小的节点,并返回,然后用这个节点的值赋值删除节点的key和value // 右子树中key最小的节点一定不含左子树,所以删除这个key最小的节点一定是属于叶子节点或者只有右子树的节点 Node directPostNode = this.getDirectPostNode(currentNode); currentNode.key = directPostNode.key; currentNode.value = directPostNode.value; } return true; } // 获取到待删除节点的中序直接后继节点。将该后继节点从二叉树中删除并返回 @Override public Node getDirectPostNode(Node delNode) { // TODO Auto-generated method stub // 方法作用为得到待删除节点的直接后继节点 Node parentNode = delNode;// 用来保存待删除节点的直接后继节点的父亲节点 Node direcrPostNode = delNode;// 用来保存待删除节点的直接后继节点 Node currentNode = delNode.rightChild;// 待删除节点右子树 while (currentNode != null) { parentNode = direcrPostNode; direcrPostNode = currentNode; currentNode = currentNode.leftChild; } if (direcrPostNode != delNode.rightChild) {// 从树中删除此直接后继节点 parentNode.leftChild = direcrPostNode.rightChild;// 后继节点的父节点指向后继节点的右孩子 direcrPostNode.rightChild = null;// 直接后继节点右孩子为空 } return direcrPostNode;// 返回此直接后继节点 }
// 前序遍历树 @Override public void preOrder(Node rootNode) { // TODO Auto-generated method stub if (rootNode != null) { System.out.println(rootNode.key + " " + rootNode.value); this.preOrder(rootNode.leftChild); this.preOrder(rootNode.rightChild); } }
// 中序遍历树 @Override public void inOrder(Node rootNode) { // TODO Auto-generated method stub if (rootNode != null) { this.inOrder(rootNode.leftChild); System.out.println(rootNode.key + " " + rootNode.value); this.inOrder(rootNode.rightChild); } }
// 后序遍历树 @Override public void postOrder(Node rootNode) { // TODO Auto-generated method stub if (rootNode != null) { this.postOrder(rootNode.leftChild); this.postOrder(rootNode.rightChild); System.out.println(rootNode.key + " " + rootNode.value); } } /** * // 基于二叉排序树查找find查找节点,然后通过Node的setValue将新值赋值过去。 */ @Override public boolean update(int key, int value) { // TODO Auto-generated method stub Node node = this.find(key); node.setValue(value); return true; } }