简说哈希表

hash表

计算机科学中，hash table是一种重要的数据结构，它可以将键映射到值。键值通过hash函数计算后，就得到它对应的值在数组中的位置。哈希也被意译为散列。

图为 用hash表实现的电话簿。

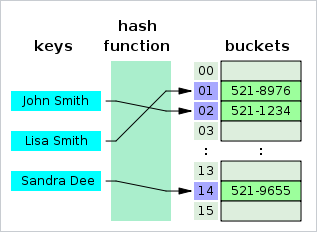
理想情况下每个键值都有属于自己的位置，但实际的哈希函数却不能做到完美，因此会导致哈希冲突，也即不同的键可能映射到相同的位置。

复杂度	平均数	最差的情况
空间	O( n )	O( n )
搜索	O(1)	O( n )
插入	O(1)	O( n )
删除	O(1)	O( n )

散列

键通过散列函数运算，就得到它对应的数组下标。

index = f(key, array_size)

这在计算机中，通常分为两个步骤，先将key通过一个hash运算，然后将运算后的值对数组长度取余。

hash = hashfunc(key)
index = hash % array_size

• 散列函数

  哈希表性能好不好取决于散列函数。在计算机中，上面拆分的两步中第二步是固定的，因此我们通常讨论的是第一步的 hashfunc 的性能。散列函数的基本要求是该函数应该提供 均匀分布的散列值，非均匀分布会增加冲突的数量和解决冲突的成本。

关键特性

哈希表的一个关键参数是负载因子 = n / k。n 是哈希表中的条目数， k 是桶的数量。

随着负载因子变大，哈希表将变慢，冲突发生概率增大。通常会有一个临界数值，达到临界后，将需要扩容。java中的HashMap默认临界负载因子是0.75，这是在时间和空间成本之间的经验权衡。

冲突处理

不同的键值哈希到同一个数组下标就产生了哈希冲突，大量数据存入哈希表中，冲突实际上是不可避免的。

所有的哈希表实现都有一些冲突解决策略来处理。

1.链接法

冲突后将冲突的数据链在原有数据后面，需要额外的指针来查找数据。

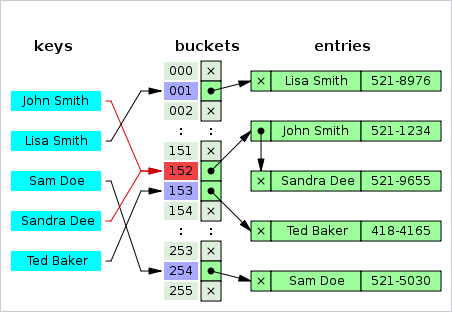
只要每个桶中元素个数不多，那么这种解决方法就能获得很好的性能。但它也继承了链表的缺点，遍历链表时缓存性能较差，因为处理器缓存容易无效。

上图是在哈希表的槽中只存指针，还有一种实现是槽中既有对象也有指针。

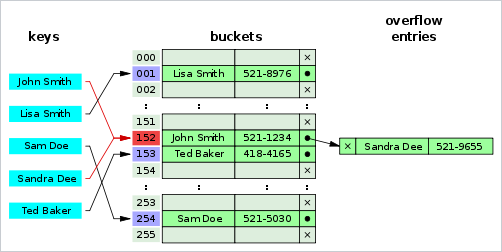
这样的实现哈希表访问的缓存效率会得到提升。而且如果没有冲突(这是多数情况)，那么不需要遍历指针，效率也更高。

java中(java8以前)的哈希表就是采用的这种策略。

更进阶的，如果考虑到冲突可能非常严重，那么链表的低效将产生很大影响，java8增加了红黑树，当链表长度达到一定值时将链表转换为红黑树，降低了查询效率。但是这样也增加了实现复杂度，以及插入删除所需要的时间。

2.开放寻址法

将地址放开使用，冲突后通过某种探测策略，直到找到一个空的槽。常见的有三种探测方法：线性探测、平方探测、再散列。

• 线性探测 ：间隔是固定的i（通常为 1）。 由于良好的CPU 缓存利用率，该算法应用最广泛。
• 二次探测：间隔是 i*i，平方探测不一定能找到空的槽。
• 再散列：通过另一个散列函数再进行一次散列

3.建立公共溢出区

为哈希表再分配一块溢出区，发生冲突的元素放进溢出区。这个貌似很少使用。

性能分析

我们可以用平均查找次数来衡量查找性能。查找性能取决于冲突的多少，影响冲突次数的因素是：

1. 散列函数是否均匀，尽量把数据等概率的分布到表中；
2. 散列表的负载因子；
3. 处理冲突的方法是否恰当。

当没有冲突的时候查找时间复杂度是O(1)，如果有冲突，最坏的情况会退至O(n)。

有两个因素会显着影响哈希表上的操作延迟：

• 缓存丢失。因为链式法，随着负载因子的增加，哈希表的搜索和插入性能会由于平均缓存丢失的增加而大幅下降。
• 调整大小的成本。当哈希表变得庞大时，调整大小成为一项极其耗时的任务。

特点

优点

• 哈希表相对于其他表数据结构的主要优势是速度。当键值对数量较大时，这种优势更加明显。当可以预测存入的数量时，哈希表特别有效，因为可以以最佳大小分配一次桶数组，并且永远不用调整大小。
• 如果键值对是固定的并且提前已知，则可以通过仔细选择散列函数、表大小和内部数据结构来降低平均查找成本。 人们甚至能够设计出一种无冲突甚至完美的散列函数。 在这种情况下，密钥不需要存储在表中。

缺点

• 虽然哈希表的操作平均时间较少，但一个好的哈希函数的成本可能明显高于顺序列表或搜索树的查找算法的内部循环。 因此当条目数量非常小时，哈希表优势无法体现。
• 哈希表中的元素遍历只能以某种伪随机顺序进行。
• 哈希表的局部性较差，因为数据几乎是随机分布的，所以容易导致缓存失效。

*参考：Hash table - Wikipedia