函数的定义与使用
>函数的理解与定义
函数是一段代码的表示
-函数是一段具有特定功能的、可重用的语句组
-函数是一种功能的抽象,一般函数表达特定功能
-两个作用:降低编程难度 和 代码复用
def <函数名>(<参数(0个或多个)>) :
<函数体>
return <返回值>
#计算n! def fact(n) : #fact 函数名;n 参数 s = 1 for i in range(1, n+1): s *= i return s # s 返回值
-函数定义时,所指定的参数是一种占位符
-函数定义后,如果不经过调用,不会被执行
-函数定义时,参数是输入、函数体是处理、结果是输出(IPO)
>函数的使用及调用过程
调用是运行函数代码的方式
#接上段代码 a=fact(10)
-调用时要给出实际参数
-实际参数替换定义中的参数
-函数调用后得到返回值
>函数的参数传递
参数个数:函数可以有参数,也可以没有,但必须保留括号
def fact() : print("我是一个没有参数的函数")
可选参数传递:函数定义时可以为某些参数指定默认值,构成可选参数
def <函数名>(<非可选参数>,<可选参数>) :
<函数体>
return <返回值>
#计算 n!//m def fact(n, m=1) : #m=1为可选参数 s = 1 for i in range(1, n+1): s *= i return s//m #fact(10) 3628800 #fact(10,5) 725760
可变参数传递
函数定义时可以设计可变数量参数,即不确定参数总数量
def <函数名>(<参数>,*b) :
<函数体>
return <返回值>
#计算 n!乘数 def fact(n, *b) : #*b可变参数 s = 1 for i in range(1, n+1): s *= i for item in b: s *= item return s # fact(10,3) 10886400 #fact(10,3,5,8) 435456000
参数传递的两种方式:函数调用时,参数可以按照位置或名称方式传递
def fact(n, m=1) : s = 1 for i in range(1, n+1): s *= i return s//m # fact( 10,5 ) 725760 # fact( m=5,n=10 ) 725760
>函数的返回值
函数可以返回0个或多个结果
-return保留字用来传递返回值
-函数可以有返回值,也可以没有,可以有return,也可以没有
-return可以传递0个返回值,也可以传递任意多个返回值
def fact(n,m=1): s=1 for i in range(1,n+1) s*=i return s//m,n,m #fact(10,5) (725760,10,5)
#a,b,c=fact(10,5)
#print(a,b,c)
#725760 10 5
>局部变量与全局变量
n, s = 10, 100 #n,s时全局变量 def fact(n) : s = 1 #fact()函数中的n s是局部变量 for i in range(1, n+1): s *= i return s print(fact(n), s) #n,s是全局变量 #3628800 100
规则1:局部变量和全局变量是不同变量
-局部变量是函数内部的占位符,与全局变量可能重名但不同
-函数运算结束后,局部变量被释放
-可以使用global保留字在函数内部使用使用全局变量
n, s = 10, 100 #n,s时全局变量 def fact(n) : global s #fact()函数中使用global保留字声明 此处s是全局变量s for i in range(1, n+1): s *= i return s print(fact(n), s) #此处全局变量s是被函数修改 #362880000 362880000
规则2:局部变量为组合数据类型且未创建,等同于全局变量
ls = ["F", "f"] #通过使用[]真实创建了一个全局变量列表ls def func(a) : ls.append(a) #此处ls是列表类型,未真实创建 则等同于全局变量 return func("C") #局部变量ls被修改 print(ls) # ['F','f','C']
ls = ["F", "f"] #通过使用[]真实创建了一个全局变量列表ls def func(a) : ls = [] #此处ls是列表类型,真实创建ls是局部变量 ls.append(a) return func("C") #局部变量ls被修改 print(ls) #['F','f']
使用规则
-基本数据类型,无论是否重名,局部变量与全局变量不同
-可以通过global保留字在函数内部声明全局变量
-组合数据类型,如果局部变量未真实创建,则是全局变量
>lambda函数
lambda函数返回函数名作为结果
-lambda函数是一种匿名函数,即没有名字的函数
-使用lambda保留字定义,函数名是返回结果
-lambda函数用于定义简单的、能够在一行内表示的函数
<函数名> = lambda <参数> : <表达式>
等价于
def <函数名> (<参数>):
<函数体>
return <返回值>
f=lambda x,y:x+y f=(10,15) #结果:25 f=lambda:"lambda函数" print(f()) #结果:lambda函数
谨慎使用lambda函数
-lambda函数主要用作一些特定函数或方法的参数
-lambda函数有一些固定的使用方式,建议逐步掌握
-一般情况,建议使用def定义的普通函数
代码复用与函数递归
>代码复用与模块化设计
把代码当成资源的抽象
-代码资源化:程序代码是一种用来表达计算的“资源”
-代码抽象化:使用函数等方法对代码赋予更高级别的定义
-代码复用:同一份代码在需要时可以被重复使用
函数 和 对象 是代码复用的两种主要形式
函数:将代码命名在代码层面建立了初步抽象
对象:属性和方法 <a>.<b> 和<a>.<b>( )在函数之上再次组织进行抽象
分而治之
-通过函数或对象封装将程序划分为 模块及 模块间的表达
-具体包括:主程序、子程序和子程序间的关系
-分而治之:一种分而治之、分层抽象、体系化的设计思想
紧耦合 松耦合
-紧耦合:两个部分之间交流很多,无法独立存在
-松耦合:两个部分之间交流少,可以独立存在
-模块内部紧耦合、模块之间松耦合
>函数递归的理解
函数定义中调用函数自身的方式

两个关键特征
-链条:计算过程存在递归链条
-基例:存在一个或多个不需要再次递归的基例
类似数学归纳法
-数学归纳法
-证明当n取第一个值n0时命题成立
-假设当nk时命题成立,证明当n=nk+1时命题也成立
-递归是数学归纳法思维的编程体现
>函数递归的调用过程

def fact(n): if n==0: return 1 else: return n*fact*(n-1)
函数+分支语句
-递归函数本身是一个函数,需要函数定义方式描述
-函数内部,采用分支语句对输入参数进行判断
-基例和链条,分别编写对应代码
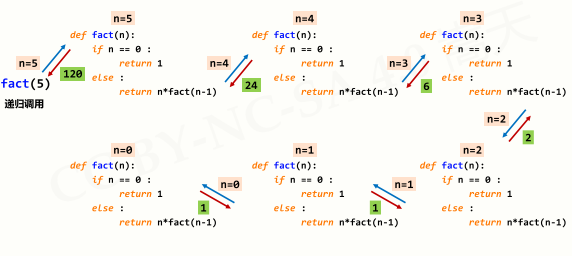
>函数递归实例解析
将字符串s反转后输出
def rvs(s): if s == "": return s slse: return rvs(s[1:])+s[0]
斐波那契数列:一个经典的数列
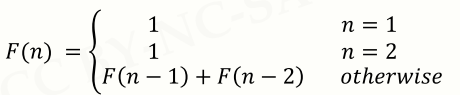
def f(n): if n==1 or n==2 : return 1 else: return f(n-1)+f(n-2)