图片压缩 DCT变换 实时视频

研究目的：理解xCode源码。

DCT变换源自付立叶级数和付立叶变换，是高等数学下册的学习内容。

可以这么理解，DCT变换是付立叶变换的一个特例。 任何一个“函数”都可以转换成付立叶级数。为什么要这样转换呢，主要是目前已经对付立叶级数的组成函数（sinx,cosx)研究的相当深入了，所以无论多么复杂的函数经过付立叶级数的转换成，可以轻松的分析它的很多特性。

网上搜了很多的内容，大部分都写“DCT变换将时域信号转变为频域信号”，其实这样的说明主要指的是与时间相关的信号。例如：

 

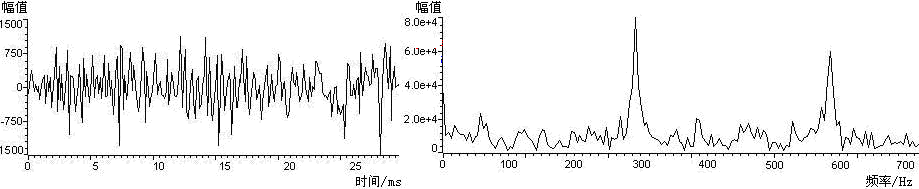
左图就是时域图，右图是频域图。

时域图就是振幅随时间的变化关系，频域图是振幅随频率的变化关系。可以看出，频率在哪个范围内振幅比较大。

以上这种分析主要体现在电子电路的信号分析上，在音频的分析上也会用到。那么图片压缩为什么要转换成到频域呢？

BMP图像是一个二维的信号集，每一个信号代表二维集里的一个点。目前的计算机将每一个点都用24位或32位来表示。这样就极大地增加了存储空间。

那么经过DCT变换后，也会产生如上图所示的效果，而且效果更有特点。

一张普通的图片（为了说明方便，假设图片的每一个点，都以一个整数表示）。经过DCT转换后，只有左上角的信号大于0，其余的大部分信号都接近0。

用图片表示如下：

 

从如上图可以看出，经过DCT变换后，原来的图像信号都集中在的左上解。其余大部分是0。网上也有说法是只有低频信号的起作用，高频信号可以忽略不计。网上说的低频与高频源自对DCT变换公式的理解。

 

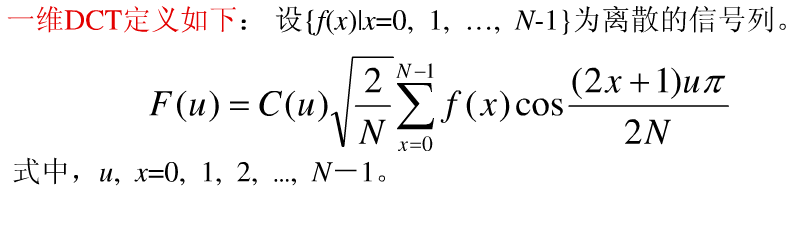
 当x的值越取越大，（2x+1)也越大，频率就会越大，反应在图片上的位置也就越靠近右下角，因为他接近于0，所以说可以忽略不计。这样为图片的高比率压缩提供了技术保证。所以目前DCT变换在图片压缩（JPEG）及实时传输（x264）方面被广泛应用。

上面所说的图片压缩用到的DCT变换都是二维变换，要深刻理解DCT变换，首先从一维变换开始，以下是按公式进行的一维变换的记录。

变换前：
0.000000        1.000000        2.000000        3.000000        4.000000
5.000000        6.000000        7.000000        8.000000        9.000000

变换后：
14.230249       -9.024851       -0.000001       -0.966656       -0.000001
-0.316227       -0.000001       -0.127870       -0.000001       -0.035856

逆变换：
0.000000        1.000000        2.000000        3.000000        4.000000
5.000000        6.000001        7.000000        8.000001        8.999998
请按任意键继续. . .

去除高频后的结果如下：（因为测试数据量少，所以效果不太明显）。

变换前：
0.000000        1.000000        2.000000        3.000000        4.000000
5.000000        6.000000        7.000000        8.000000        9.000000

变换后：
14.230249       -9.024851       -0.000001       -0.966656       -0.000001
-0.316227       -0.000001       -0.127870       -0.000001       -0.035856

去除高频：
14.230249       -9.024851       -0.000001       -0.966656       -0.000000
-0.000000       -0.000000       -0.000000       -0.000000       -0.000000

逆变换：
0.128470        0.836239        1.951775        3.094658        4.064886
4.935114        5.905343        7.048225        8.163761        8.871529
请按任意键继续. . .

总结：

1、DCT变换为可逆，无损失变换。

2、DCT变换可过虑掉高频信号，以达到数据有损压缩的目的，高频信号过虑得越多压缩比越高，损失也越严重。

3、DCT变换运算量很大，需要用快速DCT变换以提高变换效率。

 

根据公式写的一维变换，代码如下：

#include "stdafx.h"
#include <string.h>
#include <iostream>
#include <math.h>

using namespace std;
#define PI 3.1415926

int _tmain(int argc, _TCHAR* argv[])
{
    double        dInput[] = {0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0};
    int            iFactor[] = {1, 1, 1, 1, 0, 0, 0, 0, 0, 0};
    double        dOut[10] = {0};
    double        dOut1[10]= {0};
    const int N = sizeof(dInput)/sizeof(double);

    for (int u=0; u<N; u++)
    {
        for (int x=0; x<N; x++)
        {
            if (u == 0)
                dOut[u]+= dInput[x] * cos((2*x + 1)*PI*u/(2*N)) / sqrt((double)N);
            else
                dOut[u]+= dInput[x] * cos((2*x + 1)*PI*u/(2*N)) * sqrt(2.0) / sqrt((double)N);
        }
    }
    printf("\n变换前：\n");
    for (int i=0; i<N; i++)
    {
        printf("%f\t", dInput[i]);
    }

    printf("\n变换后：\n");
    for (int i=0; i<N; i++)
    {
        printf("%f\t", dOut[i]);
    }

    printf("\n去除高频：\n");
    for (int i=0; i<N; i++)
    {
        dOut[i] *= iFactor[i];
        printf("%f\t", dOut[i]);
    }

    printf("\n逆变换：\n");
    for (int x=0; x<N; x++)
    {
        for (int u=0; u<N; u++)
        {
            if (u == 0)
                dOut1[x]+= dOut[u] * cos((2*x + 1)*PI*u/(2*N)) /sqrt((double)N);
            else
                dOut1[x]+= dOut[u] * cos((2*x + 1)*PI*u/(2*N)) * sqrt(2.0) / sqrt((double)N);
        }
    }

    for (int i=0; i<N; i++)
    {
        printf("%f\t", dOut1[i]);
    }
}