前言
什么是高精度?
高精度是一种算法,用于计算各种大数的运算。
什么意思呢?
我举个栗子。首先OI界有一句金玉良言:
即使题面出的水,只要数据够变态,难度指数级上升。
对于著名的水题和各种神仙的装弱工具A+B Problem,它的数据范围是什么呢?
(|a|,|b| le 10^9)
嗯,所以我们可以放心大胆的这么写:
#include <iostream>
#include <cstdio>
int main() {
int a,b;
std :: cin >> a >> b;
std :: cout << a + b << std :: endl;
return 0;
}
但是,如果我把数据范围改成这样:
(|a|,|b| le 10^{18})
你就不能用int了,而得用long long:
#include <iostream>
#include <cstdio>
int main() {
long long a,b;
std :: cin >> a >> b;
std :: cout << a + b << std :: endl;
return 0;
}
最后,我要是把数据范围改成这样:
(0 le a,b le 10^{500})
这就是luogu p1601的原题。
你根本就找不到一种数据类型能存这样大的数。
那怎么办呢?自己造一种数据类型?
没错,就是这样。这种算法,就叫做高精度。
面对这样大的数,蟹蟹唯一想到的办法,就是用数组存储每一个位数。
但这样,肯定不能直接加减乘除运算,我们得自定义。
怎么自定义呢?
想想我们小时候求加减乘除的方法。没错,列竖式。
同样的,这里我们也用两个需要进行运算的数进行竖式模拟运算。这种方法虽然笨,但真的没有什么别的方法了。
怎么来写高精度呢?具体的竖式应该如何去操作呢?
请接着看。
说明一下,现在noip很少考到高精度了,但是我们为了保险,还是学习一下高精度。学总比不学强嘛。
再说明:本教程中的高精度只涉及到非负整数。负数和浮点数本教程中不考虑。
正式开始(最初版本)
准备工作
首先我们需要准备好程序构架。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cassert>
const int maxn = 4005;//运算时最多的位数,也就是说这个值取决于数据范围中运算过程中数值可能的最大位数。
int main() {
}
然后定义一个结构体。这是一种高阶玩法,到头来我们可以直接用ubigint定义数,来进行高精度的运算,到时候直接加加减减就ok。
struct ubigint() {
}
赋值运算符
首先我们来看一些基本的赋值:
int s[maxn], len;
//一些基础的东西
ubigint() { memset(s, 0, sizeof(s)); }
ubigint(int num) { *this = num; }
ubigint(char *num) { *this = num; }
ubigint operator = (int num) {
char c[maxn];
sprintf(c, "%d", num);
*this = c;
return *this;
}
ubigint operator = (const char *num) {
len = strlen(num);
for(int i = 0; i < len; i++)
s[i] = num[len - i - 1] - '0';//请注意这里是倒过来赋值的,也就是说得到的数组其实直接输出,数是反着的。为什么呢?一般我们列竖式都是从后往前的,所以我们把数组进行倒序处理,这样我们在程序中就可以正序遍历了。
return *this;
}
这些都是最基本的定义赋值之类的东西,我不再赘述。
关系运算符
接下来我们来重载一些关系运算符:
//关系运算符
bool operator < (const ubigint &b) const {
if(len != b.len) return len < b.len;//比位数
for(int i = len - 1; i >= 0; i--)//诸位比较
if(s[i] != b.s[i])
return s[i] < b.s[i];
return false;
}
bool operator > (const ubigint &b) const {return b < *this; }
bool operator <= (const ubigint &b) const {return !(b < *this);}
bool operator >= (const ubigint &b) const {return !(*this < b);}
bool operator == (const ubigint &b) const {return !(b < *this) && !(b > *this);}
bool operator != (const ubigint &b) const {return b < *this || *this < b;}
我解释一下小于号。二年级数学中就有两个数比较大小的方法,先比位数,后从高位到低位诸位比较。
位数就是两个数组的长度,如果len < b.len证明小于号判断成立,如果len > b.len说明小于号判断不成立。
如果位数相等,从高位到低位诸位比较,如果当前数字不一样,则对当前的数字的大小关系来判断这两个数的大小关系。
如果诸位比较完成,说明两个数相等。不过这个时候是不满足小于的,所以返回false。
然后其他的就是各种套用小于号,因为我懒得在写一遍了qaq(不要打蟹蟹呀嘤嘤嘤)
算术运算符
加法
首先先来康加法。
首先小学我们是咋算加法的呢?对了,列竖式。
我们可以从最后一位(再次提醒,请注意本教程中数组存储是倒着的,所以程序中是从第一个字符开始遍历)开始无脑加法,然后把得到的结果放在结果的对应位置。
吗?
你在想什么啊,进位我们还得考虑。
于是,我们就可以相加,如果没进位直接放,如果进位了把得到的结果%10放到结果的那个位置,然后那个位置的前面那个位置加上1(表示进位)。
但是我们显然还漏掉了一种情况,当两个加数的位数不相同。其实这个问题根本不算什么问题,只需要特判好了。
这样就不难得到代码了:
ubigint operator + (const ubigint &b) const {
ubigint res;
res.len = 0;
for(int i = 0, x = 0; x || i < len || i < b.len; i++, x /= 10) {
if(i < len) x += s[i];
if(i < b.len) x += b.s[i];
res.s[res.len++] = x % 10;
}
return res;
}
减法
然后是减法。
减法其实和加法差不多,也是按位相减,如果不够,借1.
顺便说明一下,这里的减法不支持被减数小于减数的情况,也就是结果必须大于0.
ubigint operator - (const ubigint &b) const {
assert(*this >= b);
ubigint res;
res.len = 0;
int x;
for(int i = 0, g = 0; i < len; i++) {
x = s[i] - g;
if(i < b.len) x -= b.s[i];
if(x >= 0) g = 0;
else {
x += 10;
g = 1;
}
res.s[res.len++] = x;
}
res.clear_zero();//注意到这里了没有?
return res;
}
如果你是一个细心的人,会发现上面多了一个clear_zero()。
这是什么?
一般在高精度运算中,可能会出现结果是正确的,但是结果之前有好几个0.这种0叫做前导0,高精度运算中常常不能避免,所以我们需要定义一个clear_zero()函数去掉这些多余的前导0.
怎么清呢?我们只需要定义这样的代码:
void clear_zero() {
while(len > 1 && !s[len - 1]) len--;
}
你可能会问了,为什么是len > 1,而不是len > 0呢?
前导0不是遇到不是0的情况才停的,你想啊,如果这个数是0,那这个0可不算是前导0.所以我们不清个位,个位都有前导0只能说明这个数是0,需要特殊对待。
乘法
乘法这点就比较难了,蟹蟹陪你耐心分析。(其实也不是很难辣,放松心态呀qaq)
小学我们是怎么学的?每一位按位相乘,相乘的结果再进行相加。
但存储相乘的结果又是一笔开销,我们不如思维跳跃一下,把每一位相乘的结果直接对应到res数组里,岂不美滋滋?
这里我们有一个定律,第一个数从后往前第i位数 和 第二个数从后往前第j位数 相乘 的结果 最后 会相加到 结果的 从后往前第i+j位上。
如果你不懂,不如先列几个竖式,感受感受下?这里一定要弄懂哦。
但是进位也是个麻烦事。每一位的数在枚举i,j的时候随时都会变,随时进位总觉得不好。我们还是都累积完了,再一一进位吧,这样比较好。(个人习惯辣)
于是就有了如下的代码:
ubigint operator * (const ubigint &b) const {
ubigint res;
res.len = len + b.len;
for(int i = 0; i < len; i++)
for(int j = 0; j < b.len; j++)
res.s[i + j] += s[i] * b.s[j];
for(int i = 0; i < res.len - 1; i++) {
res.s[i + 1] += res.s[i] / 10;
res.s[i] %= 10;
}
res.clear_zero();
return res;
}
除法
其实除法就是乘法的逆运算,和乘法也差不多,就像加法和减法一样。不过除法在试除这个方面是有技巧的,我们可以二分试除。
ubigint operator / (const ubigint &b) const {
assert(b > 0);
ubigint res = *this,m;
for(int i = len - 1; i >= 0; --i) {
m = m * 10 + s[i];
res.s[i] = midsearch(b, m);
m = m - b * res.s[i];
}
res.clear_zero();
return res;
}
midsearch函数:
int midsearch(const ubigint &b, const ubigint &m) const {
int L = 0, R = 9, mid;
while(1) {
mid = (L + R) >> 1;
if(b * mid <= m) {
if(b * (mid + 1) > m) return mid;
else L = mid;
}
else R = mid;
}
}
模法
除法都完了,但是别忘了,我们还有魔法。我不会告诉你这其实是%法的,%%% tql orz
取模运算其实特别简单,把上述代码中,最后return m;就可以了。
ubigint operator % (const ubigint &b) const {
assert(b > 0);
ubigint res = *this;
ubigint m;
for(int i = len - 1; i >= 0; i--) {
m = m * 10 + s[i];
res.s[i] = midsearch(b,m);
m = m - b * res.s[i];
}
m.clear_zero();
return m;
}
扩展赋值运算符
我们还可以通过以上的五则运算,扩展出+= -= *= /= %= 。 这就很简单辣。
ubigint& operator += (const ubigint &b) {*this = *this + b; return *this;}
ubigint& operator -= (const ubigint &b) {*this = *this - b; return *this;}
ubigint& operator *= (const ubigint &b) {*this = *this * b; return *this;}
ubigint& operator /= (const ubigint &b) {*this = *this / b; return *this;}
ubigint& operator %= (const ubigint &b) {*this = *this % b; return *this;}
输入输出流
最后的最后,我们搞定输入输出流吧。
std :: istream& operator >>(std :: istream &in, ubigint &x) {
std :: string s;
in >> s;
x = s.c_str();
return in;
}
std :: ostream& operator <<(std :: ostream &out,ubigint x) {
out << x.to_str();
return out;
}
哦对了差点忘记说,我们为了输出ubigint这个类型,还需要定义一个to_str函数,把ubigint类型转成std :: string型。很简单辣。
std :: string to_str() {
std :: string res = "";
for(int i = 0; i < len; i++) res = (char)(s[i] + '0') + res;
return res;
}
至此我们的ubigint就定义完了,拍张合照!
总体代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cassert>
const int maxn = 30005;
struct ubigint {
int s[maxn], len;
//一些基础的东西
ubigint() { memset(s, 0, sizeof(s)); }
ubigint(int num) { *this = num; }
ubigint(char *num) { *this = num; }
ubigint operator = (int num) {
char c[maxn];
sprintf(c, "%d", num);
*this = c;
return *this;
}
ubigint operator = (const char *num) {
len = strlen(num);
for(int i = 0; i < len; i++)
s[i] = num[len - i - 1] - '0';
return *this;
}
int midsearch(const ubigint &b, const ubigint &m) const {
int L = 0, R = 9, mid;
while(1) {
mid = (L + R) >> 1;
if(b * mid <= m) {
if(b * (mid + 1) > m) return mid;
else L = mid;
}
else R = mid;
}
}
std :: string to_str() {
std :: string res = "";
for(int i = 0; i < len; i++) res = (char)(s[i] + '0') + res;
return res;
}
void clear_zero() {
while(len > 1 && !s[len - 1]) len--;
}
//关系运算符
bool operator < (const ubigint &b) const {
if(len != b.len) return len < b.len;
for(int i = len - 1; i >= 0; i--)
if(s[i] != b.s[i])
return s[i] < b.s[i];
return false;
}
bool operator > (const ubigint &b) const {return b < *this; }
bool operator <= (const ubigint &b) const {return !(b < *this);}
bool operator >= (const ubigint &b) const {return !(*this < b);}
bool operator == (const ubigint &b) const {return !(b < *this) && !(b > *this);}
bool operator != (const ubigint &b) const {return b < *this || *this < b;}
ubigint operator + (const ubigint &b) const {
ubigint res;
res.len = 0;
for(int i = 0, x = 0; x || i < len || i < b.len; i++, x /= 10) {
if(i < len) x += s[i];
if(i < b.len) x += b.s[i];
res.s[res.len++] = x % 10;
}
return res;
}
ubigint operator - (const ubigint &b) const {
assert(*this >= b);
ubigint res;
res.len = 0;
int x;
for(int i = 0, g = 0; i < len; i++) {
x = s[i] - g;
if(i < b.len) x -= b.s[i];
if(x >= 0) g = 0;
else {
x += 10;
g = 1;
}
res.s[res.len++] = x;
}
res.clear_zero();
return res;
}
ubigint operator * (const ubigint &b) const {
ubigint res;
res.len = len + b.len;
for(int i = 0; i < len; i++)
for(int j = 0; j < b.len; j++)
res.s[i + j] += s[i] * b.s[j];
for(int i = 0; i < res.len - 1; i++) {
res.s[i + 1] += res.s[i] / 10;
res.s[i] %= 10;
}
res.clear_zero();
return res;
}
ubigint operator / (const ubigint &b) const {
assert(b > 0);
ubigint res = *this,m;
for(int i = len - 1; i >= 0; i--) {
m = m * 10 + s[i];
res.s[i] = midsearch(b, m);
m = m - b * res.s[i];
}
res.clear_zero();
return res;
}
ubigint operator % (const ubigint &b) const {
assert(b > 0);
ubigint res = *this;
ubigint m;
for(int i = len - 1; i >= 0; i--) {
m = m * 10 + s[i];
res.s[i] = midsearch(b,m);
m = m - b * res.s[i];
}
m.clear_zero();
return m;
}
ubigint& operator += (const ubigint &b) {*this = *this + b; return *this;}
ubigint& operator -= (const ubigint &b) {*this = *this - b; return *this;}
ubigint& operator *= (const ubigint &b) {*this = *this * b; return *this;}
ubigint& operator /= (const ubigint &b) {*this = *this / b; return *this;}
ubigint& operator %= (const ubigint &b) {*this = *this % b; return *this;}
};
std :: istream& operator >>(std :: istream &in, ubigint &x) {
std :: string s;
in >> s;
x = s.c_str();
return in;
}
std :: ostream& operator <<(std :: ostream &out,ubigint x) {
out << x.to_str();
return out;
}
int main() {
}
压位优化
其实这样的高精度我们还能继续优化。来看下面这个例子:
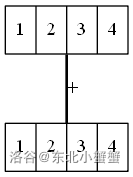
显然我们在ubigint类中,是一位一位加的。但是我们为什么不能这样??
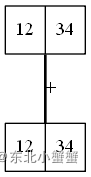
之前算四遍,现在算两遍。我们可以想想,能不能直接算一遍呢?
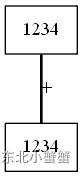
行吧,这就是直接算了。
但是我们为什么不能这样直接算一遍呢?这其实就是高精度存在的意义,根本不存在一种数据方式来算这么大的加法。比如以下就是一个例子:

这可不能直接算。但是我们有刚刚的方法,可以尽量的分割这两个数:
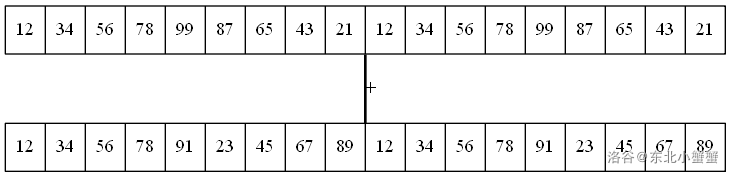
这样算的话,就变成了两位两位的算,算的次数减少了,就会有优化。
我们还可以压4位:
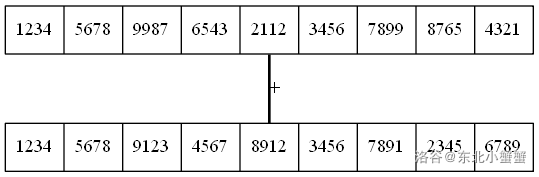
算的方法就更少啦。
我们不妨思考一个问题,我们这样分数,分得的每一个区域允许的最大位数是多少?
如果是int型,显然是9位。因为int的范围最大是2147483647,此时9位相加相减,不会爆炸。所以我们最好这样:

这种方法,就叫做压位。使用压位的高精,就叫做压位高精。
平常我们所说的压x位,其实就是把数分成若干部分,使得每一个部分最大是x位数。(为什么是最大呢,因为有可能没分完。)
有好奇心强的小伙伴可能会问了,压位看起来算的次数减少,可每一个位置内置的加法算法不是也增多了吗?这样岂不是拆东墙补西墙?
我谔谔,C++内置的加法算法怎么说也是经过层层优化的,增加位数并不会浪费多长的时间,至少不像我们写的高精度,要不然C++也走不到这样高的巅峰。我们有更高的靠山,就尽量去靠。
代码:
/*
* @Author: crab-in-the-northeast
* @Date: 2020-03-19 23:07:41
* @Last Modified by: crab-in-the-northeast
* @Last Modified time: 2020-03-19 01:07:24
*/
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cassert>
#include <cstring>
#include <string>
int max(int a,int b) {
return a > b ? a : b;
}
static const int base = 1000000000;
static const int width = 9;
struct ubigint {
typedef long long ll;
ll s[8005] = {0};
int len = 1;
ubigint(){}
ubigint(const ubigint& x) {
for(int i = 0; i < x.len; i++)
this -> s[i] = x.s[i];
this -> len = x.len;
}
ubigint(const int& x) {
int tmp = x;
this -> len = 0;
do{
this -> s[this -> len++] = tmp % base;
tmp /= base;
}while(tmp);
}
ubigint operator = (const std :: string& str) {
std :: string tmp = str;
while(tmp.length() > width) {
this -> s[this -> len - 1] = atoi(tmp.substr(tmp.length() - width).c_str());
tmp.erase(tmp.length() - width);
this -> len++;
}
this -> s[this -> len - 1] = atoi(tmp.c_str());
return *this;
}
void clear_zero() {
while(this -> len > 1 && !(this -> s[this -> len - 1])) this -> len--;
}
ubigint operator = (const ubigint& x) {
this -> len = x.len;
for(register int i = 0; i < this -> len; i++)
this -> s[i] = x.s[i];
return *this;
}
bool operator < (const ubigint& b) const {
if(this -> len != b.len) return this -> len < b.len;
for(register int i = this -> len - 1; i >= 0; i--)
if(this -> s[i] != b.s[i])
return this -> s[i] < b.s[i];
return false;
}
bool operator > (const ubigint& b) const {
return b < *this;
}
bool operator <= (const ubigint& b) const {
return !(b < *this);
}
bool operator >= (const ubigint& b) const {
return !(*this < b);
}
bool operator != (const ubigint& b) const {
return *this < b || b < *this;
}
bool operator == (const ubigint& b) const {
return !(b < *this) && !(*this < b);
}
ubigint operator + (const ubigint& b) const {
ubigint res;
res.len = max(this -> len, b.len);
for(register int i = 0, last = 0; i < res.len; i++) {
res.s[i] = this -> s[i] + b.s[i] + last;
last = res.s[i] / base;
res.s[i] %= base;
if(i == res.len - 1 && last) res.len++;
}
res.clear_zero();
return res;
}
ubigint operator - (const ubigint& b) const {
assert(*this >= b);
ubigint res = *this;
for(register int i = 0, last = 0; i < this -> len; i++) {
res.s[i] -= b.s[i] + last;
if(res.s[i] < 0) {
res.s[i] += base;
last = 1;
}else last = 0;
}
res.clear_zero();
return res;
}
ubigint operator * (const ubigint& b) const {
if(*this == 0 || b == 0) return ubigint(0);
//if(*this == 1) return b;
//if(b == 1) return *this;
ubigint res;
res.len = this -> len + b.len + 1;
for(register int i = 0; i < this -> len; i++) {
for(register int j = 0; j < b.len; j++) {
res.s[i + j] += this -> s[i] * b.s[j];
res.s[i + j + 1] += res.s[i + j] / base;
res.s[i + j] %= base;
}
}
res.clear_zero();
return res;
}
ubigint operator / (const ubigint& b) const {
if(b > *this) return 0;
//if(b == *this) return 1;
ubigint res = 0, div = b, mod = *this;
while(div * ubigint(base) <= *this) div *= ubigint(base);
for(;;) {
int l = 1, r = base, mid;
if(mod >= div) {
while(r > l + 1) {
int mid = l + r >> 1;
if(div * ubigint(mid) > mod) r = mid;
else l = mid;
}
mod -= div * ubigint(l);
res.s[res.len - 1] += l;
}
if(div == b) break;
res.len++;
for(register int i = 1; i < div.len; i++)
div.s[i - 1] = div.s[i];
div.s[div.len - 1] = 0;
div.len--;
}
std :: reverse(res.s, res.s + res.len);
res.clear_zero();
return res;
}
ubigint operator % (const ubigint& b) const {
return *this - (*this / b * b);
}
ubigint operator += (const ubigint& b) {*this = *this + b; return *this;}
ubigint operator -= (const ubigint& b) {*this = *this - b; return *this;}
ubigint operator *= (const ubigint& b) {*this = *this * b; return *this;}
ubigint operator /= (const ubigint& b) {*this = *this / b; return *this;}
ubigint operator %= (const ubigint& b) {*this = *this % b; return *this;}
friend std :: istream& operator >> (std :: istream& in, ubigint& b) {
std :: string str;
in >> str;
b = str;
return in;
}
friend std :: ostream& operator << (std :: ostream& out, ubigint b) {
out << b.s[b.len - 1];
for(register int i = b.len - 2; i >= 0; i--) {
int div = base / 10;
while(b.s[i] < div) {
std :: cout << 0;
div /= 10;
}
if(b.s[i]) out << b.s[i];
}
return out;
}
};
int main() {
ubigint a,b;
std :: cin >> a >> b;
std :: cout << a + b << std :: endl;
if(a >= b) std :: cout << a - b << std :: endl;
else std :: cout << '-' << b - a << std :: endl;
std :: cout << a * b << std :: endl;
std :: cout << a / b << std :: endl;
std :: cout << a % b << std :: endl;
return 0;
}
这是静态数组版本的,我们还可以用动态数组vector来重构代码。不过这样时间需要的就长啦(写这个的时候懒得写this ->了qvq)
#include <iostream>
#include <cstdio>
#include <cstring>
#include <string>
#include <cassert>
#include <vector>
int max(int a,int b) {
return a > b ? a : b;
}
struct ubigint {
typedef unsigned long long ull;
static const int base = 100000000;
static const int width = 8;
std :: vector<int> s;
ubigint& clear_zero() {
while(!s.back() && s.size() > 1) s.pop_back();
return *this;
}
ubigint(ull num = 0) {*this = num;}
ubigint(std :: string str) {*this = str;}
ubigint& operator = (ull num) {
s.clear();
do {
s.push_back(num % base);
num /= base;
}while(num);
return *this;
}
ubigint& operator = (const std :: string& str) {
s.clear();
int x;
int len = (str.length() - 1) / width + 1;
for(int i = 0; i < len; i++) {
int endidx = str.length() - i * width;
int startidx = max(0, endidx - width);
int x;
sscanf(str.substr(startidx, endidx - startidx).c_str(), "%d", &x);
s.push_back(x);
}
return (*this).clear_zero();
}
bool operator < (const ubigint& b) const {
if(s.size() != b.s.size()) return s.size() < b.s.size();
for(int i = s.size() - 1; i >= 0; i--)
if(s[i] != b.s[i])
return s[i] < b.s[i];
return false;
}
bool operator > (const ubigint& b) const {return b < *this; }
bool operator <= (const ubigint& b) const {return !(b < *this);}
bool operator >= (const ubigint& b) const {return !(*this < b);}
bool operator == (const ubigint& b) const {return !(b < *this) && !(b > *this);}
bool operator != (const ubigint& b) const {return b < *this || *this < b;}
ubigint operator + (const ubigint& b) const {
ubigint res;
res.s.clear();
for(int i = 0, x = 0; x || i < s.size() || i < b.s.size(); i++, x /= base) {
if(i < s.size()) x += s[i];
if(i < b.s.size()) x += b.s[i];
res.s.push_back(x % base);
}
return res.clear_zero();
}
ubigint operator - (const ubigint& b) const {
assert(*this >= b);
ubigint res;
res.s.clear();
for(int i = 0, last = 0;last || i < s.size() || i < b.s.size();i++) {
int x = s[i] + last;
if(i < b.s.size()) x -= b.s[i];
if(x < 0) {
last = -1;
x += base;
}else last = 0;
res.s.push_back(x);
}
return res.clear_zero();
}
ubigint operator * (const ubigint& b) const {
std :: vector<ull> tmp(s.size() + b.s.size(),0);
ubigint res;
res.s.clear();
for(int i = 0; i < s.size(); i++)
for(int j = 0; j < b.s.size(); j++)
tmp[i + j] += ull(s[i]) * b.s[j];
ull last = 0;
for(int i = 0; last || i < tmp.size(); i++) {
ull x = tmp[i] + last;
res.s.push_back(x % base);
last = x / base;
}
return res.clear_zero();
}
int midsearch(const ubigint& b, const ubigint& m) const {
int l = 0, r = base - 1;
while(1) {
int mid = l + r >> 1;
if(b * mid <= m && b * (mid + 1) > m) return mid;
if(b * mid <= m) l = mid;
else r = mid;
}
}
ubigint operator / (const ubigint& b) const {
assert(b > 0);
ubigint res = *this, mod;
for(int i = s.size() - 1; i >= 0; i--) {
mod = mod * base + s[i];
res.s[i] = midsearch(b, mod);
mod -= b * res.s[i];
}
return res.clear_zero();
}
ubigint operator % (const ubigint& b) const {
assert(b > 0);
ubigint res = *this, mod;
for(int i = s.size() - 1; i >= 0; i--) {
mod = mod * base + s[i];
res.s[i] = midsearch(b, mod);
mod -= b * res.s[i];
}
return mod.clear_zero();
}
ubigint& operator += (const ubigint& b) {*this = *this + b; return *this;}
ubigint& operator -= (const ubigint& b) {*this = *this - b; return *this;}
ubigint& operator *= (const ubigint& b) {*this = *this * b; return *this;}
ubigint& operator /= (const ubigint& b) {*this = *this / b; return *this;}
ubigint& operator %= (const ubigint& b) {*this = *this % b; return *this;}
friend std :: istream& operator >> (std :: istream& in, ubigint& x) {
std :: string str;
if(!(in >> str)) return in;
x = str;
return in;
}
friend std :: ostream& operator << (std :: ostream& out, ubigint x) {
out << x.s.back();
for(int i = x.s.size() - 2; i >= 0; i--) {
char buf[20];
sprintf(buf, "%08d", x.s[i]);
for(int j = 0; j < strlen(buf); j++)
out << buf[j];
}
return out;
}
};
ubigint a,b;
int main() {
std :: cin >> a >> b;
std :: cout << a + b << std :: endl;
if(a >= b) std :: cout << a - b << std :: endl;
else std :: cout << "-" << b - a << std :: endl;
std :: cout << a * b << std :: endl;
std :: cout << a / b << std :: endl;
std :: cout << a % b << std :: endl;
return 0;
}
当然这样的高精度还存在一些不足,比如不支持负数,乘法没有FFT优化等。但是考虑到竞赛中不会出现这么duliu的高精度,本文不作处理。
小试牛刀
最后我们来小试几道牛刀吧。
luogu p1601(高精A + B):
int main() {
ubigint a, b;
std :: cin >> a >> b;
std :: cout << a + b << std :: endl;
return 0;
}
luogu p2142(高精A - B):
这道题需要负数诶!不过没关系,我们有一个小伎俩:
int main() {
ubigint a,b;
std :: cin >> a >> b;
if(a < b) std :: cout << "-" << b - a << std :: endl;
else std :: cout << a - b<< std :: endl;
return 0;
}
是不是既简单又方便的偷懒方式呢~
luogu p1303(高精A * B):
int main() {
ubigint a, b;
std :: cin >> a >> b;
std :: cout << a * b << std :: endl;
return 0;
}
luogu p1480 & luogu p2005(高精A / B):
后面的那个是前面的那个的升级版。双倍经验美滋滋
int main() {
ubigint a,b;
std :: cin >> a >> b;
std :: cout << a / b << std :: endl;
return 0;
}
luogu p1932(高精合集):
int main() {
ubigint a,b;
std :: cin >> a >> b;
std :: cout << a + b << std :: endl;
if(a >= b) std :: cout << a - b << std :: endl;
else std :: cout << '-' << b - a << std :: endl;
std :: cout << a * b << std :: endl;
std :: cout << a / b << std :: endl;
std :: cout << a % b << std :: endl;
return 0;
}
因为原题中的减法涉及到了负数,所以减法做了这样的处理qvq(别打我啊qvq)
而且注意,亲测本题如果用动态数组版本是无法AC的,结果是80TLE,必须得吸氧才能AC。所以这道题请使用静态数组版本。
luogu p1009(阶乘之和):
int main() {
int n;
ubigint ans;
std :: cin >> n;
for(int i = 1; i <= n; i++) {
ubigint mul = 1;
for(int j = 2; j <= i; j++)
mul *= j;
ans += mul;
}
std :: cout << ans << std :: endl;
return 0;
}
luogu p1591(阶乘数码,一个数的阶乘中某个数码出现了几次):
直接按照题意模拟,没啥好说的吧qaq。
int main() {
int T;
std :: cin >> T;
while(T--) {
int n, num, ans = 0;
std :: cin >> n >> num;
ubigint res = 1;
for(int i = 2; i <= n; i++)
res *= i;
ull tmp = res.s.back();
while(tmp) {
if(tmp % 10 == num) ans++;
tmp /= 10;
}
for(int i = res.s.size() - 2; i >= 0; i--) {
char buf[20];
sprintf(buf, "%08d", res.s[i]);
for(int j = 0; j < strlen(buf); j++)
if(buf[j] - '0' == num) ans++;
}
std :: cout << ans << std :: endl;
}
}
luogu p1255(数楼梯):
此题的主要思路是递推,套上了高精度的外衣而已。但是这个过于简单就归于高精模板里吧。
const int maxn = 5005;
int n;
ubigint a[maxn] = {0, 1, 2};
int main() {
std :: cin >> n;
if(n <= 2) {
std :: cout << a[n] << std :: endl;
return 0;
}
for(int i = 3; i <= n; i++)
a[i] = a[i - 1] + a[i - 2];
std :: cout << a[n] << std :: endl;
return 0;
}
qvq别忘了点个赞再走呀qvq!