[BZOJ3730]震波

题目

  点这里看题目。
   BZOJ 目测......是炸了。

分析

  动态点分治入门题。
  首先理解什么叫 " 动态点分治 "。
  一般点分治需要离线解决，不带修改。动态点分治可以用点分治的方法在线解决问题，支持修改。
  在点分治的过程中，每个点都会成为一次分治中心进行计算。如果我们将点按照计算顺序连成一棵树的话，我们就会得到原树的一颗 " 虚树 " ， 我们称之为点分树。煮个栗子：
  可以发现，由于重心的先天性质，点分树的树高为$O(log_2n)$。
  对于本题，由于只会有单点修改（例如修改$u$），所以我们可以在点分树上从$u$开始，对于$u$到点分树的根的路径进行暴力修改，这样只会有$O(log_2n)$个点。再深的点不会受到影响（因为对于更深的点，它们进行点分治的时候，$u$已经没有了）。
  如何维护信息？我们对于点分树上每一个点$u$维护两个树状数组，第一个树状数组维护下标为到$u$距离的权值和，用于直接计算贡献；第二个树状数组维护下标为到$u$点分树上父亲距离的权值和，用于容斥扣除重复贡献。统计的方式类似于修改，我们在点分树上从$u$开始上跳，用树状数组计算贡献。再煮个栗子：

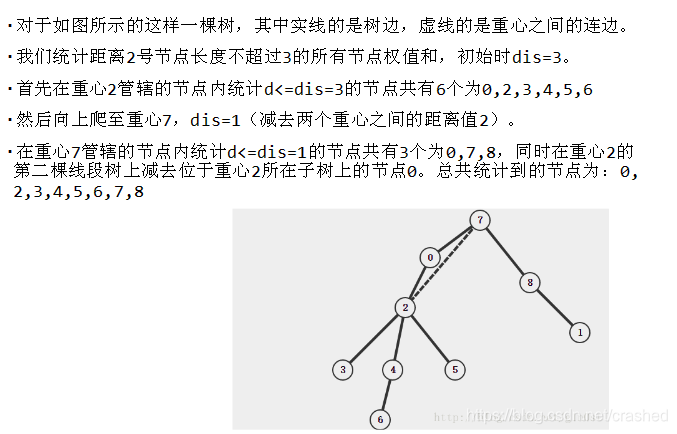
  现在想必各位都懂了。
  需要注意的几点：
  1. 注意点分树上，祖先到自己的距离并不是单调递增的。因此不能中途 break。
  2. 由于我们只需要知道点分树上祖先到自己的距离和祖先的标号，且点分树深度有限，因此我们把这两个值用数组存下来即可。
  3. 树状数组需要用 vector 存。仅存下需要的空间会优化到$O(nlog_2n)$（跟点分治基础时间复杂度一样），而不优化会变成$O(n^2)$， MLE。
  4. 树状数组注意下标不要变成非正数。
  5. 函数千万千万不要传 vector 的值！！！亲测会慢 10 倍！！！

代码

#include <map>
#include <cmath>
#include <vector>
#include <cstdio>
#include <cstring>
using namespace std;

const int MAXN = 1e5 + 5, MAXLOG = 20;

template<typename _T>
void read( _T &x )
{
	x = 0;char s = getchar();int f = 1;
	while( s > '9' || s < '0' ){if( s == '-' ) f = -1; s = getchar();}
	while( s >= '0' && s <= '9' ){x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar();}
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ){ putchar( '-' ); x = ( ~ x ) + 1; }
	if( 9 < x ){ write( x / 10 ); }
	putchar( x % 10 + '0' );
}

template<typename _T>
_T MAX( const _T a, const _T b )
{
	return a > b ? a : b;
}

template<typename _T>
_T MIN( const _T a, const _T b )
{
	return a < b ? a : b;
}

struct edge
{
	int to, nxt;
}Graph[MAXN << 1];

vector<int> BIT[MAXN][2]; 

int f[MAXN][MAXLOG], dis[MAXN][MAXLOG];
int siz[MAXN], dep[MAXN], mx[MAXN];
int head[MAXN], curVal[MAXN], val[MAXN];
int N, M, all, cnt;
bool vis[MAXN];

int lowbit( const int &x ) { return x & ( -x ); }
void upt( int &x, const int v ) { x = MAX( x, v ); }
bool visible( const int u, const int fa ) { return u ^ fa && ! vis[u]; }

void update( const int u, const int t, int x, const int v )
{
	int lim = BIT[u][t].size() - 1;
	for( ; x <= lim && x ; x += lowbit( x ) ) BIT[u][t][x] += v;
}

int getSum( const int u, const int t, int x )
{
	x = MIN( x, ( int ) BIT[u][t].size() - 1 ); int ret = 0;
	for( ; x > 0 ; x -= lowbit( x ) ) ret += BIT[u][t][x];
	return ret;
}

void addEdge( const int from, const int to )
{
	Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
	head[from] = cnt;
}

int getCen( const int u, const int fa )
{
	int ret = 0, tmp; siz[u] = 1, mx[u] = 0;
	for( int i = head[u], v ; i ; i = Graph[i].nxt )
		if( visible( v = Graph[i].to, fa ) )
		{
			tmp = getCen( v, u );
			siz[u] += siz[v], mx[u] = MAX( mx[u], siz[v] );
			if( mx[tmp] < mx[ret] ) ret = tmp;
		}
	mx[u] = MAX( mx[u], all - siz[u] );
	if( mx[u] < mx[ret] ) ret = u;
	return ret;
}

void DFS( const int u, const int fa, const int rt, const int d )
{
	for( int i = head[u], v ; i ; i = Graph[i].nxt )
		if( visible( v = Graph[i].to, fa ) )
			dis[v][++ dep[v]] = d, f[v][dep[v]] = rt,
			DFS( v, u, rt, d + 1 );
}

void divide( const int u )
{
	vis[u] = true; DFS( u, 0, u, 1 );
	int tmp = all;
	BIT[u][0].resize( tmp + 1 ), BIT[u][1].resize( tmp + 1 );
	for( int i = head[u], v ; i ; i = Graph[i].nxt )
		if( ! vis[v = Graph[i].to] )
		{
			all = siz[v]; if( all > siz[u] ) all = tmp - siz[u];
			divide( getCen( v, u ) );
		}
}

void change( const int u, const int nVal )
{
	int dif = nVal - curVal[u]; curVal[u] = nVal;
	update( u, 1, dis[u][dep[u]], dif );
	for( int i = dep[u] ; i ; i -- )
		update( f[u][i], 0, dis[u][i], dif ),
		update( f[u][i], 1, dis[u][i - 1], dif );
}

int query( const int u, const int k )
{
	int ret = getSum( u, 0, k ) + curVal[u];
	for( int i = dep[u] ; i ; i -- )
		if( dis[u][i] <= k )
		{
			ret += getSum( f[u][i], 0, k - dis[u][i] ) + curVal[f[u][i]];
			ret -= getSum( f[u][i + 1], 1, k - dis[u][i] );
		}
	return ret;
}

int main()
{
	read( N ), read( M );
	for( int i = 1 ; i <= N ; i ++ ) read( val[i] );
	for( int i = 1, a, b ; i < N ; i ++ ) read( a ), read( b ), addEdge( a, b ), addEdge( b, a );
	mx[0] = all = N; divide( getCen( 1, 0 ) );
	for( int i = 1 ; i <= N ; i ++ ) f[i][dep[i] + 1] = i;
	for( int i = 1 ; i <= N ; i ++ ) change( i, val[i] );
	int op, a, b, lst = 0;
	while( M -- )
	{
		read( op ), read( a ), read( b );
		a ^= lst, b ^= lst;
		if( op ) change( a, b );
		else write( lst = query( a, b ) ), putchar( '
' );
	}
	return 0;
}