[HDU6864] Jumping on a Cactus

题目

点这里看题目。

分析

首先我们对边进行定向：从 (d) 小的指向 (d) 大的。于是我们就一定会得到一个 DAG（参考题目条件）。

问题就相当于是求出这个 DAG 的拓扑序的方案数。

众所周知，这个问题目前还没有多项式算法，所以我们就可以弃题了

且慢，我们的图原先是一个仙人掌。仙人掌就相当于是要分别考虑环和树：

树

显然我们可以直接树形 DP 。考虑 (g(u)) 为以 (u) 为根的子树的拓扑序方案数。

跟几乎所有的树形 DP 一样，我们需要考虑合并两棵子树。设两棵子树的根为 (u) 和 (v) 。设以 (u) 为根的子树大小为 (s_u) 。

我们只需要考虑合并对应的拓扑序，显然合并结果 (res) 就是

[res=inom{s_u+s_v}{s_u} imes g(u) imes g(v) ]

需要注意的是，我们在计算 (g(u)) 的时候，应当钦定 (u) 为子树拓扑序的第一个，否则是不合法的。

环

根据题目条件，我们知道仙人掌上面只有偶环。

那么我们就取仙人掌上面 (d) 最小的点 (x) 和最大的点 (y) ：

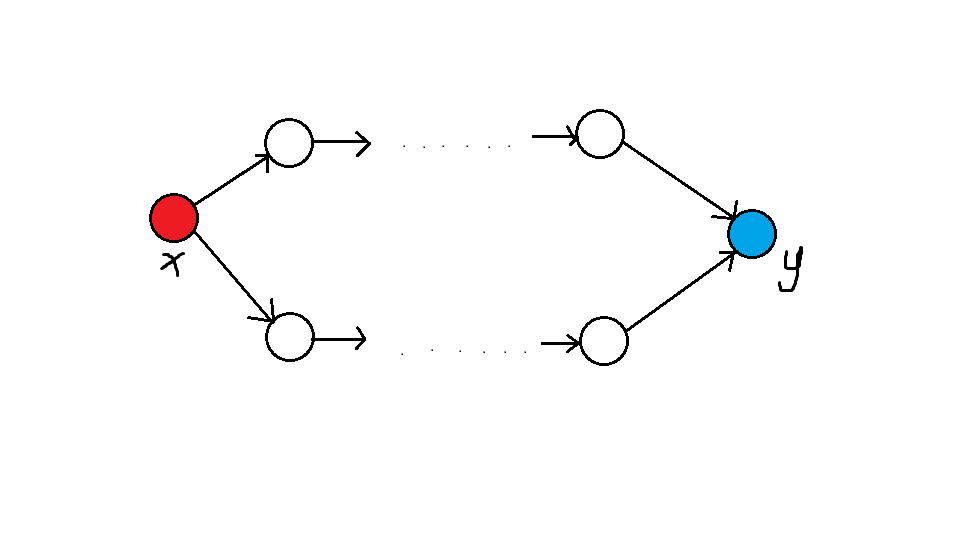
建立拓扑序的时候，我们一定会先进入 (x) 。于是拆掉它，图就变成了......两只"耳朵"的造型。

此时两只"耳朵"是互不影响的。我们只需要选取哪个"耳朵"的第一个的 (p) 更小，于是就可以考虑 DP 。

(f(i,j))：一只耳朵长 (i) ，另一只长 (j) 时候的方案数。

以" (i) 的第一个的 (p) 更小"的情况为例。我们记这个点为 (u) ，此时它的未合并的"子树"大小为 (s_u) （包括了 (u)）：

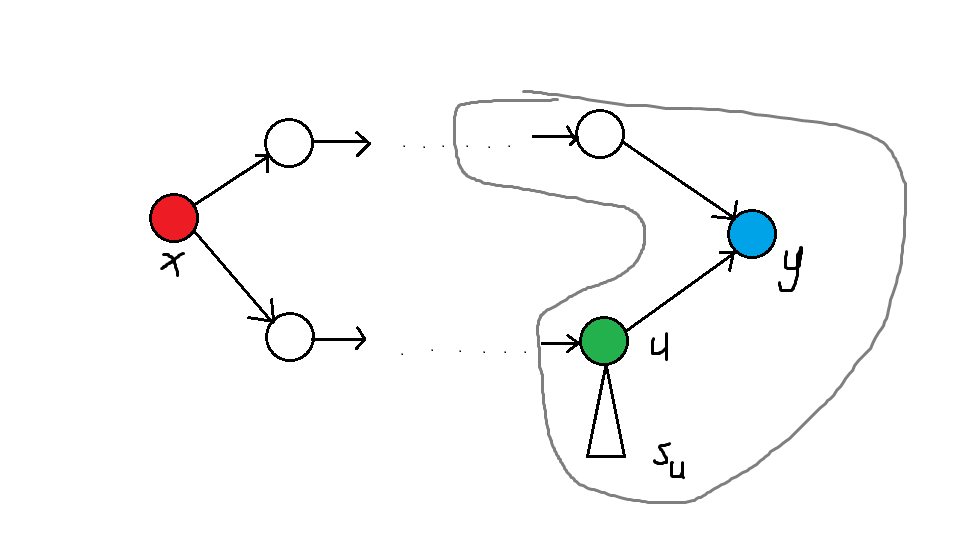
首先我们钦定了 (u) 在此时的拓扑序最小。然后考虑将 (u) 的"子树"合并到 (f(i-1,j)) 的拓扑序上来。可以发现 (f(i,j)) 的拓扑序的长度就是银色圈圈内的 (s) 之和，记之为 (tot)。

参考树的部分。我们不难写出此时的贡献就是：

[res=inom{tot-1}{s_u-1} imes f(i-1,j) imes g(u) ]

然后暴力 DP 就是了。

仙人掌

不难想到建立圆方树来更好地处理仙人掌。我们可以将一条边看作长度为 2 的环，那么就有圆方交替出现。我们只需要将方点最终的 (f) 值记为它的 (g) ，就可以很方便地转移了。

胡说，我明明写了 160 行。

时间是 (O(n^2)) 。

本题的一些有价值的点：

1. 对序列 DP ，通常考虑序列的合并。这通常就要用到二项式系数来合并。

2. 将仙人掌拆成环和边"分而治之"，然后再凑回仙人掌。

3. 圆方树一定要开两倍空间，清空的时候一定要清到两倍。

代码

#include <cstdio>

typedef long long LL;

const int mod = 998244353;
const int MAXN = 2e4 + 5;

template<typename _T>
void read( _T &x )
{
	x = 0;char s = getchar();int f = 1;
	while( s > '9' || s < '0' ){if( s == '-' ) f = -1; s = getchar();}
	while( s >= '0' && s <= '9' ){x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar();}
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ){ putchar( '-' ); x = ( ~ x ) + 1; }
	if( 9 < x ){ write( x / 10 ); }
	putchar( x % 10 + '0' );
}

template<typename _T>
_T MIN( const _T a, const _T b )
{
	return a < b ? a : b;
}

struct Graph
{
	struct edge
	{
		int to, nxt;
	}Gra[MAXN << 1];
	
	int head[MAXN];
	int cnt;
	
	void nxt( int &x ) const { x = Gra[x].nxt; }
	edge& operator [] ( const int &x ) { return Gra[x]; }
	void Clr( const int n ) { cnt = 0; for( int i = 1 ; i <= n ; i ++ ) head[i] = 0; }
	void Add( const int from, const int to ) { AddEdge( from, to ), AddEdge( to, from ); }
	
	void AddEdge( const int from, const int to )
	{
		Gra[++ cnt].to = to, Gra[cnt].nxt = head[from];
		head[from] = cnt;
	}
}G, T;

int fac[MAXN], ifac[MAXN];

int seq[MAXN], siz1[MAXN], siz2[MAXN], len;
int stk[MAXN], top;

int f[MAXN >> 1][MAXN >> 1], g[MAXN], siz[MAXN];
int DFN[MAXN], LOW[MAXN];
int N, M, tot, sta, ID;

int Sub( int x, const int v ) { return x < v ? x + mod - v : x - v; }
int Mul( LL x, const int v ) { x *= v; if( x >= mod ) x %= mod; return x; }
int Add( int x, const int v ) { return x + v >= mod ? x + v - mod : x + v; }
int C( const int n, const int m ) { return n < m ? 0 : Mul( fac[n], Mul( ifac[m], ifac[n - m] ) ); }

int Qkpow( int base, int indx )
{
	int ret = 1;
	while( indx )
	{
		if( indx & 1 ) ret = Mul( ret, base );
		base = Mul( base, base ), indx >>= 1;
	}
	return ret;
}

void Tarjan( const int u, const int fa )
{
	stk[++ top] = u;
	DFN[u] = LOW[u] = ++ ID;
	for( int i = G.head[u], v ; i ; G.nxt( i ) )
		if( ( v = G[i].to ) ^ fa )
		{
			if( ! DFN[v] ) 
			{
				Tarjan( v, u ), LOW[u] = MIN( LOW[u], LOW[v] );
				if( LOW[v] >= DFN[u] )
				{
					tot ++;
					do T.Add( tot, stk[top] );
					while( stk[top --] ^ v );
					T.Add( u, tot );
				}
			}
			else LOW[u] = MIN( LOW[u], DFN[v] );
		}
}

void Init()
{
	G.Clr( N << 1 ), T.Clr( N << 1 );
	top = ID = 0, tot = N;
	for( int i = 1 ; i <= N << 1 ; i ++ )
		seq[i] = stk[i] = siz[i] = siz1[i] = siz2[i] = DFN[i] = LOW[i] = 0;
}

void DFS( const int u, const int fa )
{
	if( u > N )
	{
		for( int i = T.head[u], v ; i ; T.nxt( i ) )
			if( ( v = T[i].to ) ^ fa ) 
				DFS( v, u ), siz[u] += siz[v];
		len = 0;
		for( int i = T.head[u] ; i ; T.nxt( i ) )
			seq[++ len] = T[i].to;
		int mid = len / 2 + 1;
		for( int i = 0 ; i < mid - 1 ; i ++ )
			for( int j = 0 ; j < mid - 1 ; j ++ )
				f[i][j] = 0;
		for( int i = 1 ; i < mid - 1 ; i ++ )
			siz1[i] = Add( siz1[i - 1], siz[seq[mid - i]] ),
			siz2[i] = Add( siz2[i - 1], siz[seq[mid + i]] );
		f[0][0] = g[seq[mid]];
		for( int i = 0 ; i < mid - 1 ; i ++ )
			for( int j = 0 ; j < mid - 1 ; j ++ )
				if( i + j )
				{
					int cnt = siz1[i] + siz2[j] + siz[seq[mid]] - 1;
					if( i ) f[i][j] = Add( f[i][j], Mul( C( cnt, siz[seq[mid - i]] - 1 ), Mul( f[i - 1][j], g[seq[mid - i]] ) ) );
					if( j ) f[i][j] = Add( f[i][j], Mul( C( cnt, siz[seq[mid + j]] - 1 ), Mul( f[i][j - 1], g[seq[mid + j]] ) ) );
				}
		g[u] = f[mid - 2][mid - 2];
	}
	else
	{
		siz[u] = 0, g[u] = 1;
		for( int i = T.head[u], v ; i ; T.nxt( i ) )
			if( ( v = T[i].to ) ^ fa )
			{
				DFS( v, u );
				g[u] = Mul( C( siz[u] += siz[v], siz[v] ), Mul( g[u], g[v] ) );
			}
		siz[u] ++;
	}
}

int main()
{
	fac[0] = 1;
	for( int i = 1 ; i <= 10000 ; i ++ ) fac[i] = Mul( fac[i - 1], i );
	ifac[10000] = Qkpow( fac[10000], mod - 2 );
	for( int i = 9999 ; ~ i ; i -- ) ifac[i] = Mul( ifac[i + 1], i + 1 );
	
	int T;
	read( T );
	while( T -- )
	{
		read( N ), read( M ), read( sta ), Init();
		for( int i = 1, a, b ; i <= M ; i ++ ) 
			read( a ), read( b ), G.Add( a, b );
		Tarjan( sta, 0 );
		DFS( sta, 0 );
		write( g[sta] ), putchar( '
' );
	}
	return 0;
}