[CF1495F] Squares

题目

点这里看题目。

分析

考虑做不来就该直接赛后看题解。

下面称花费为 (a) 的移动为小跳，花费为 (b) 的移动为大跳。

考虑 (i) 这个位置被经过，必须要满足，对于任意 (j<i,p_j>p_i) ， (j) 都被经过（我们可以认为 (p_0=n+1) ）。

注意到对于最右边的一个 (j) ， (j) 要被经过，也要满足类似的条件。这意味着我们只需要在图上建立链式的结构就可以表示 (i) 的限制；多个链式的结构，凑在一起，就变成了一棵树。

下图展示了 (p=[2,1,5,3,4]) 的树形结构（图源官方题解）

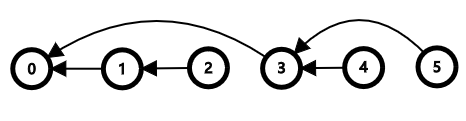
对于这棵树，基本分析如下：

0. 0 一定会被经过。

1. 如果 (i) 要被经过，那么 (i) 的祖先一定都会选择小跳。

2. 如果 (i) 这里选择了大跳，就相当于直接跳过 (i) 的子树而进入到了它相邻下一个兄弟。

因此，可以单独考虑小跳的节点集合 (S) （其他节点为大跳或不经过）。

根据上面的分析，可以知道 (S) 一定为包含 0 的一棵子树。

针对某一特定的 (S) ，可以得到花费为：

[sum_{uin S}a_u+sum_{u ot=S,fa_uin S}b_u ]

简单地做一下差分使各项独立——设 (c_x=a_x-b_x+sum_{fa_y=x}b_y) ，那么花费可以改写成：

[sum_{uin S}c_u ]

回过头来考虑题目的限制，可以发现它等价于强制 (S) 必须包含某棵以 0 为根的子树。那么我们可以用 set 在 DFS 序上面维护一下强制要选的部分的和，剩下的，则可以预处理出每一个子树的最优选法的和，然后计算一下^[1]。

时间就是 (O((n+q)log_2n)) 。

小结：

1. 将原题的限制转化成树形结构，联系祖先，确实是很巧的方法。
2. 差分技巧的使用。

代码

#include <set>
#include <cmath>
#include <cstdio>
using namespace std;

#define rep( i, a, b ) for( int i = (a) ; i <= (b) ; i ++ )
#define per( i, a, b ) for( int i = (a) ; i >= (b) ; i -- )

typedef long long LL;
typedef set<int> :: iterator Iter;

const int MAXN = 2e5 + 5, MAXLOG = 20;

template<typename _T>
void read( _T &x )
{
	x = 0;char s = getchar();int f = 1;
	while( s > '9' || s < '0' ){if( s == '-' ) f = -1; s = getchar();}
	while( s >= '0' && s <= '9' ){x = ( x << 3 ) + ( x << 1 ) + ( s - '0' ), s = getchar();}
	x *= f;
}

template<typename _T>
void write( _T x )
{
	if( x < 0 ){ putchar( '-' ); x = ( ~ x ) + 1; }
	if( 9 < x ){ write( x / 10 ); }
	putchar( x % 10 + '0' );
}

struct Edge
{
	int to, nxt;
}Graph[MAXN << 1];

set<int> s;

int buc[MAXN];
bool vis[MAXN];

int f[MAXN][MAXLOG];
LL su[MAXN], bst[MAXN];
int DFN[MAXN], dep[MAXN], seq[MAXN], head[MAXN];
int stk[MAXN], top;

int A[MAXN], B[MAXN], P[MAXN];
int N, Q, cnt, lg2, ID; LL ans = 0;

void AddEdge( const int from, const int to )
{
	Graph[++ cnt].to = to, Graph[cnt].nxt = head[from];
	head[from] = cnt;
}

void DFS( const int u, const int fa )
{
	seq[DFN[u] = ++ ID] = u;
	dep[u] = dep[fa] + 1, f[u][0] = fa;
	for( int i = head[u], v ; i ; i = Graph[i].nxt )
		if( ( v = Graph[i].to ) ^ fa )
		{
			DFS( v, u ), su[u] += B[v];
			if( bst[v] < 0 ) bst[u] += bst[v], bst[v] = 0;
		}
	bst[u] += A[u] - B[u] + su[u];
}

void Init()
{
	DFS( 0, 0 ), lg2 = log2( N );
	rep( j, 1, lg2 ) rep( i, 1, N ) 
		f[i][j] = f[f[i][j - 1]][j - 1];
	rep( i, 2, N ) bst[seq[i]] += bst[f[seq[i]][0]];
}

void Balance( int &u, const int stp )
{
	for( int i = 0 ; ( 1 << i ) <= stp ; i ++ )
		if( stp >> i & 1 ) u = f[u][i];
}

int LCA( int u, int v )
{
	if( dep[u] > dep[v] ) Balance( u, dep[u] - dep[v] );
	if( dep[v] > dep[u] ) Balance( v, dep[v] - dep[u] );
	if( u == v ) return u;
	per( i, lg2, 0 ) if( f[u][i] ^ f[v][i] ) u = f[u][i], v = f[v][i];
	return f[u][0];
}

LL Dist( const int u, const int v ) { return bst[u] + bst[v] - 2 * bst[LCA( u, v )]; }

void Insert( const int u )
{
	Iter it = ( s.insert( DFN[u] ), s.find( DFN[u] ) );
	int pre = 0, nxt = 0;
	if( it != s.begin() ) pre = seq[* -- it]; it ++;
	if( it != s.end() && ( ++ it ) != s.end() ) nxt = seq[* it];
	ans += Dist( u, pre ) + Dist( u, nxt ) - Dist( pre, nxt );
}

void Delete( const int u )
{
	set<int> :: iterator it = s.find( DFN[u] );
	int pre = 0, nxt = 0; 
	if( it != s.end() ) 
	{
		it ++;
		if( it != s.end() )
			nxt = seq[* it];
		it --;
	}
	if( it != s.begin() ) pre = seq[* -- it];
	ans -= Dist( u, pre ) + Dist( u, nxt ) - Dist( pre, nxt );
	s.erase( DFN[u] );
}

int main()
{
	read( N ), read( Q );
	rep( i, 1, N ) read( P[i] );
	rep( i, 1, N ) read( A[i] );
	rep( i, 1, N ) read( B[i] );
	for( int i = 1 ; i <= N ; i ++ )
	{
		while( top && P[stk[top]] <= P[i] ) top --;
		AddEdge( stk[top], i ), stk[++ top] = i;
	}
	Init();
	for( int cur ; Q -- ; )
	{
		read( cur );
		if( vis[cur] )
		{
			vis[cur] = false;
			if( ! ( -- buc[f[cur][0]] ) )
				Delete( f[cur][0] );
		}
		else
		{
			vis[cur] = true;
			if( ! ( buc[f[cur][0]] ++ ) )
				Insert( f[cur][0] );
		}
		write( ans / 2 + bst[0] ), putchar( '
' );
	}
	return 0;
}

---

1. 实际上这里 (c) 可以直接预处理成子树内的最优解，然后将被父亲选中的子树的 (c) 改成 0 就 OK 了。 ↩︎